筆者はド文系で、高校程度の数学も怪しいところがたくさんあり、変なことを書いている可能性があるので注意。どうでもいい話題も多いのでまじめに読まないように。
まず、エンベロープは打弦/撥弦楽器（ピアノやギターなど）を想定した考え方だということを知っておく。詳しくは後述するが、パイプやリードにはディケイやサステインの考え方があまり馴染まない。
下の図のように、音の強さを縦軸、時間経過を横軸に取ったグラフのことをエンベロープという
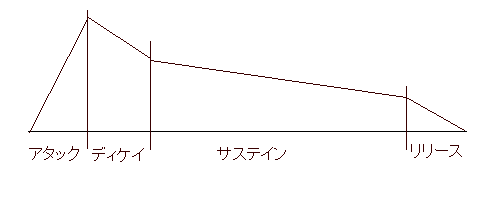
音が立ち上がるまでの範囲をアタック、急に減衰して安定するまでをディケイ、ゆっくりと減衰しながら音が持続する部分をサステイン、音が消える部分をリリースという。縦軸をレベル、横軸をタイムと呼び、アタックタイムとかサステインレベルなどという（レベルは区画内の最大音量を指すことが多い：ピアノの場合、サステインをタイムで把握しても意味がないので、たいていレートで把握する）。また、グラフの傾きをレートと呼び、サステインレートとかリリースレートなどという。レベル/タイム＝レートなので、レベル・タイム・レートのうち2つが決まれば、残りの1つも自動的に決まる。
ピアノの場合、アタックの最初（グラフの左端）で鍵盤を押し（＝弦をハンマーで叩き）、サステインの終わりまで鍵盤を押したままにして、サステインとリリースの境界線で鍵盤を放して（＝弦をミュートして）いることになる。同じ強さで鍵盤を押した場合でも、サステインは鍵盤を押したままにすることで、リリースはハーフペダルにすることでかなり伸ばすことができるが、アタックやディケイはシフトペダルなどで少し変えられる程度。
上記の区分は絶対的なものではなく、たとえばダンパペダルを完全に踏み込んだまま鍵盤を押した場合、サステインレートとリリースレートがほぼ等しくなり、両者を区別する意味がなくなる（鍵盤とペダルを両方放したときからリリースに入る、と考えてもよいが、そうするとハーフペダルはどうするのかという問題が出てくる：あまりムキにならない方がよい）。ギターのブラッシングなども、ディケイとサステインとリリースの区別が曖昧になる。
時間経過により音色はかなり変化する（打弦/撥弦楽器に特徴的な変化）。
このため、イコライザでハイを落とすとアタックレベルが下がる。ハイをカットしないリバーブをプリディレイなしでかけてやると、結果的にアタックタイムが伸びるとともにアタックポイント（アタックとディケイの境界部分）がぼやける。ハイをカットしたリバーブだとリリースタイムが伸びる。ハイをカットしてかつプリディレイつきでリバーブをかけてやると、サステインレベルが上がってリリースタイムが大きく伸びる。ピアノをはじめ打楽器はアタックの特性を変えにくいので、これらのイフェクトで調整してやるとよい（上記以外にコンプでの調整も可能：もう少し複雑な使い方のページを参照）。リバーブは、パラ出ししてエンベロープシェイパーでアタックを削ってやっても面白い（アタック感を損なわずに残響のみ得る）。
太鼓/シンバル系の打楽器は、打弦/撥弦楽器と似たような扱いができる。たとえばライドシンバルなら、スティックで叩いた瞬間からアタックが始まり、音が立ち上がってディケイに移り、比較的安定した音量でゆっくり減衰するサステインが続き、そのまま無音に移行または手ミュートでリリースに移行、といった解釈ができる。ミュートの瞬間にノイズが出る場合は、リリースに入る直前に一瞬音量が上がることになる（ハイハットのペダルミュートが代表例：実はピアノなどでも、ハンマーや鍵盤が戻った音などが出て似たような現象は生じている）。ミュートしたまま音を出す場合（ハイハットクローズのほか、軽く手ミュートしたままライドを叩くとか、スネアのヘッドをスティックで押さえつつもう片方のスティックで叩くとか）やバスドラムを踏みっぱなす場合については、ギターのブラッシングなどと同様あまり深く考えない方がよいだろう。
吹奏楽器は、打弦/撥弦楽器に比べてアタックタイムが長く、アタック/リリース時にピッチが微妙に変わるものが多い。擦弦楽器も似たような特性（ただし、弦に弓をトンと当てて音を出し始めれば普通にディケイするし、吹奏楽器でもフルートなどはディケイの考え方が馴染む）。クレッシェンドを表現できる楽器の場合、サステインは想定してもあまり意味がない（擦弦楽器なら「弓を弦から離しているが左手はミュートしていない時間」という意味で使えなくもなさそうだが、やはりムキにならない方がよいと思う：その場合「弓を動かしている時間」はホールドと呼びたいのだが、アタックポイントのぼかし方を指す用法がある程度定着しているようでめんどくさい）。
オルガン類はアフタータッチや足ポンプや音量ペダルなどでクレッシェンドを表現でき、電気オルガン（ハモンドオルガン）はとくにアタックが速い。実機の電気オルガンの場合、アタックの瞬間だけでなくリリースの瞬間にもスイッチングノイズが乗る（電子オルガンでも、これをシミュレートできるものが多い）。サステインを想定して云々するよりは、レスリーシミュレータの特性を考えた方が有用だろう。
ヴォーカルは、ヘタクソだとアタックレベルが過大になりがち。また、マイク録音時特有の事情として、吹かれによるポップノイズがアタックに重なることもある。サステインは想定しなくてよいだろうが、出している声を一瞬で遮断することはできないので、リリースを考える意味がまったくないわけではない（個人差があるとはいえ、ピアノやギターの箱よりはかなり柔らかい素材なので、高音の減衰が急激だと思われる：実用上は、体内で発生するリリース音よりもリバーブテールの方がはるかに重要）。
シンセなどでは、生楽器の音を考えるときとは異なる独特の考え方（シンセメーカーによって一定しない）を用いることが多いようだ。
交流電流に対する抵抗（に相当するもの）で、通例Zで表す。追記：この記事よりもはるかにわかりやすい解説（トップ）を見つけたので、そちらを参照した方がよいかもしれない。
力がかかったときの反応が鈍いか鋭いか、という議論（そのものではないが）に近い考え方で、音響インピーダンスや機械インピーダンスといった応用概念もある（音が出る原理のページを参照）。硬いばね（ローインピーダンス）と柔らかいばね（ハイインピーダンス）の喩えもよく使われる。
なお、同軸ケーブルの性能表示などで目にする特性インピーダンスというのは導体の抵抗値ではなく、外部導体の内径と内部導体の直径と誘電体の比誘電率によって決まる「無損失かつ無限長を仮定した場合の、ケーブル内の電圧と電流の比」のこと（これも比喩的な概念）。出力元と入力先で信号の位相が有意にずれるくらいの長距離or高周波域で、減衰や反射などの問題に関わる（線路長が波長の1/4を超える＝位相差π/2くらいから考慮すべきとすることが多い）。
式で表すと
Z=R+Xj
Rはレジスタンス（直流に対する抵抗と同じ）、Xはリアクタンス（交流にのみ作用する抵抗で、周波数fの関数になる）、jは虚数単位を表す（通常の抵抗と周波数によって振る舞いが変わる抵抗を分けて考えるために複素数にするのが慣例）。
コンデンサにおいては2πfC（これをアドミッタンスと呼びYで表す）の逆数（容量性リアクタンス）、コイルにおいては2πfL（誘導性リアクタンス）がXになる。Lはインダクタンス（電磁誘導の大きさを表わす）でCはキャパシタンス（静電容量）を表す。
つまり、コンデンサでは容量が小さく周波数が低い（＝電流の流れ方が直流に近い）ほど大きな抵抗となり、コイルでは巻き数が多く周波数が高いほど大きな抵抗になる。
コイルやコンデンサの効果とは別に表皮効果というものもあって、周波数の高い電流ほど導線の表面近くしか流れないという現象が起こる。つまり、高周波では導線の断面積が一部しか有効利用されない（抵抗が大きくなる）。オーディオケーブルに音性信号を流す場合の表皮深さ（電流が表面電流の1/e≒0.37倍になる深さ：表皮厚とも）は0.数mm～数mmくらいのオーダー（あまり太い線を使うとハイの減衰が目立つので、普通は細い線を何本か並列に繋ぐ）。
具体的な話に入る前に基礎知識の整理を。
電力（P）は仕事率を指し、単位はワット（W）でジュール/秒（J/s）と同義。ワット秒（W・s）はジュールと互換でエネルギー量の単位。
電流（I）は荷電粒子の量で、単位はアンペア（A）でクーロン/秒（C/s）と同義。1クーロンは電子約6.24×10^18個（電子1molは96485クーロン：ファラデー定数）。電力をP=EIと表現することがあるが、第一義的にはP=(I^2)Rである（オームの法則よりE=IR：仕事をするのは抵抗を通過する荷電粒子であって電位差ではない）。抵抗が同じであれば、電流の2乗に比例して仕事率が大きくなることに注意。
電圧（E）は電位差を示し、単位はボルト（V）でジュール/クーロン（J/C）と同義（もっといえば、(ジュール/秒)/(クーロン/秒)とも等しいのでE=P/Aとなる）。アナログオーディオにおいては、音圧を電圧に変換して取り扱う（信号発生器は交流電源、信号受信器は電圧検出装置と見なせる）。非常に簡略化した図を以下に示す。
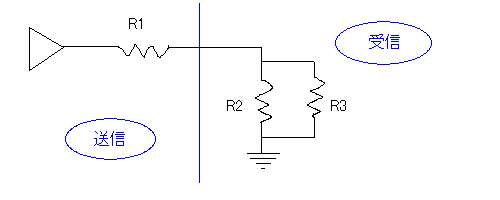
青線の左側が送信回路、右側が受信回路で、黒線がホット（信号線）、三角が交流電源、グランドはアースのように表現しているが実際にはケーブルでつないで受信側と送信側のグランド電位を共有する。R1が送信回路の内部抵抗、R2が受信回路の内部抵抗（にほぼ等しいもの）、R3が電圧計に相当する。
抵抗（R）は電流の流れにくさを示し、単位はオーム（Ω）。抵抗の逆数をジーメンス（単位S）と呼ぶ（以前はオーム（ohm）の反対なのでモー（mho）と呼び、単位もΩを上下逆さにしたものだった）。導線の抵抗などは、長さをL(m)、断面積をA(m^2)、抵抗率（もしくは比抵抗）をp(Ωm)としてR=pL/Aで求められる（抵抗率の逆数を伝導率といい、ジーメンス毎メートル（S/m）で表す）。断面積1mm^2（＝1.0×10^-6m^2）で長さ1mの導体の抵抗値はp*1000000で求められる
信号を拾う回路においては、インピーダンスが高い方が信号を受信している回路への影響が小さくなる（物理の教科書などで「抵抗が十分に高い電圧計」などと記述されているのはこのため）。
以下に、信号受信回路と検出回路（電圧計として働くので並列に入れる）のインピーダンスをそれぞれ変えた場合に全体の抵抗がどうなるかを示した。たとえば検出回路のインピーダンスが（周波数などの影響で）2倍になった場合、4000Ω＞8000Ωという動きの方が1000Ω＞2000Ωという動きよりも全体への影響が少ない。また、信号回路のインピーダンスが低い方が全体の抵抗が変わりにくい。
| 受信回路/検出回路 | 1000Ω | 2000Ω | 4000Ω | 8000Ω |
| 1Ω | 0.9990Ω | 0.9995Ω | 0.9998Ω | 0.9999Ω |
| 10Ω | 9.901Ω | 9.950Ω | 9.975Ω | 9.988Ω |
| 100Ω | 90.91Ω | 95.24Ω | 97.56Ω | 98.77Ω |
直列回路における仕事率について、電圧をV、電池の内部抵抗をR、抵抗をXR（ただしXは正の実数）として、仕事率Pを最大にするXを考えてみる。
電流I=V/(R+XR)=V/R(X+1)であり、仕事率P=I^2XR={V^2/R^2(X+1)^2}XR=XV^2/R(X+1)^2=(V^2/R){X/(X+1)^2}となる。(V^2/R)は定数とみなしているので、X/(X+1)^2の値が最大になる正の実数Xを求めればよい。ここでX/(X+1)^2>0は明らかで、逆数である(X+1)^2/Xが最小であるときX/(X+1)^2が最大となることから、結局、X+2+1/Xを最小にするX、すなわちX+1/Xを最小にするXを求めればよいことになる。よって相加相乗平均の関係からX+1/X≧2(X/X)^1/2=2で、等号成立はX=1/XすなわちX=1のとき。上記から、電池の内部抵抗（出力インピーダンス）と電池につないだ抵抗（入力インピーダンス）が等しい場合に入力側の回路での仕事率が最大になることがわかる。
参考までに、f(x)=x/(x+1)^2とすると、f(1)=1/4=0.25、f(2)=2/9≒0.22、f(4)=4/25≒0.16、f(8)=8/81≒0.10、f(16)=16/289≒0.06、f(32)=32/189≒0.03、となる。十分大きなxについてはx/(x+1)^2≒x/x^2とみなせるのでf(x)がxの逆数に近づき、十分に小さなxについてはx/(x+1)^2≒xとみなせるのでf(x)がx自体に近似する。また、f(1/x)=(1/x)/(1/X+1)^2=(1/x)/(x+1/x)^2=(1/x)(x^2/x+1)=x^2/x(x+1)=x/(x+1)なので、f(1/x)=f(x)である（つまり、電池の内部抵抗のx倍の抵抗に対する仕事率と、電池の内部抵抗のx分の1の抵抗に対する仕事率は等しい）。
たとえば、内部抵抗8Ωで起電力10Vの電池に、2Ωまたは32Ωの抵抗をつないだ場合、どちらも抵抗での仕事率は2Wになる。ただし電池内部での仕事率は同じにならず、2Ωの抵抗だと8W、32Ωの抵抗だと0.5Wになる。当然前者の方が無駄が多いし、全体の抵抗が前者では10Ω、後者では40Ωとなっていることから、前者では後者の4倍の電流が流れて回路に負担がかかる（場合によってはヒューズが飛んだり回路が壊れたりする）。
また、電池の内部抵抗が大きいと、抵抗を変更した場合に電圧が変化しやすくなる。上記の例でいうと、内部抵抗8Ωで起電力10Vの電池に32Ωの抵抗をつないだ場合抵抗にかかる電圧は8Vだが、内部抵抗8Ωで起電力10Vの電池に8Ωの抵抗をつないだ場合抵抗にかかる電圧は5Vになる。一方、電池の内部抵抗が0Ω（理想的な電池）であればどんな抵抗を接続しても常に10Vの電圧が抵抗にかかることになる。これを電源の定電圧性などと呼ぶ（物理の教科書などで「内部抵抗が十分に低い電池」などと記述されているのはこのため）。電源電圧が同じ場合、インピーダンスマッチした状態からどれだけ負荷抵抗を大きくしても、抵抗にかかる電圧は高々2倍にしかならないことに注意（すでに計算したように仕事率は低くなる）。反対に、電池の内部抵抗を無限に上げてやるとどのような抵抗をつないでも流れる電流がほぼ同じになるが、これは電源の定電流性などと呼ぶ（たとえば、内部抵抗100MΩで起電力100MVの電池があれば、50Ωの抵抗をつないでも500Ωの抵抗をつないでもほぼ1Aの電流が流れる）。
アンプにスピーカをつなぐ場合、大雑把に見るとアンプが電源でスピーカが抵抗であり、アンプが発生させた電流がスピーカのところで仕事をすることになるから、アンプ（出力）とスピーカ（入力）のインピーダンスが一致していると効率がよい。また、アンプの方がインピーダンスが高い場合は、電流は主にアンプの内部で仕事をすることになり非常に効率が悪い（というか、ショートさせたのとほぼ同じことになる）。この場合、間に抵抗（パッド）を噛ませてやると、アンプから見たスピーカのインピーダンスが高くなり（実際にはスピーカ内部だけでなく追加した抵抗のところでも電力が消費されるのだが）アンプ内部で消費される電力は少なくなる（その代わり効率が落ちる）。
あまり関係ない話だがショートといえば、乾電池をショートさせると、内部抵抗0.3Ωの単二型乾電池（1.5V）1本を直径1mm長さ20cmの銅線（常温だと長さ1mあたり0.0215Ω、導線として用いると0.025Ωくらいなので、20cmで0.005Ωとして扱う）で繋いだ場合、合計0.305Ωなので、流れる電流は約5Aとなる。内部抵抗の小さい（約0.01Ω）乗用車用の鉛蓄電池（12V）あたりだと、合計0.015Ωで800Aもの電流が流れることになる（非常に危険）。また、電池を並列に繋ぐとみかけ上の内部抵抗は低くなる。
トライテックという会社のサイトに掲載されているコラム： インピーダンスの話という解説がわかりやすいのだが、交流（面倒なのでアンバランスで考える）回路というのはつまり、ホットがグランドに落ちるまでの経路が問題なわけで、受信側には電圧計がある。
まずR1が送信側のインピーダンス、R2とR3を組み合わせたもの（この場合電圧計であるR3の抵抗値は十分に大きな値のはずなので、ほぼR2に等しい）が受信側のインピーダンスになる。送信側/受信側のインピーダンスによる効率の違いは直列回路の項で述べたとおり。また、効率（受信側での仕事率）を犠牲にして受信側のインピーダンスを高くすると、受信側にかかる電圧を比較的高くできる。R2とR3の関係でいうと、R3はR2と比較して十分に高いインピーダンスである必要がある。
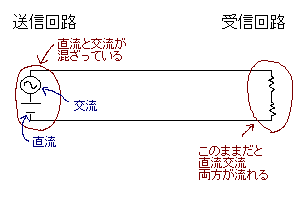
ノイズについても考えてみる。R2にかかる電圧がホットとグランドの間の電圧だけであれば、考慮するのはヒートノイズくらいでよい。ヒートノイズの電圧は抵抗値の平方根に比例して高くなる（＝抵抗値を4倍にするとヒートノイズの電圧が2倍になる）。何らかの外来ノイズがR2にかった場合は以下のようになる。
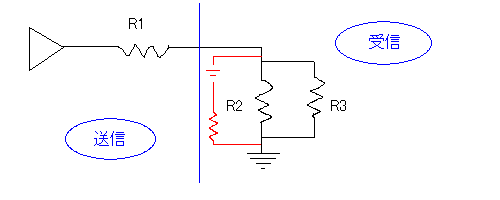
赤線の部分は、外来ノイズ（R2にかかるホット信号由来でない電圧）を仮想的な回路に見立てたもの（直流ノイズを想定した図だが、交流ノイズでも事情は同じ）。赤い仮想回路とR2が並列回路の関係になるので、R2のインピーダンスが高ければ高いほど、R2にかかるノイズ電圧も高くなる（R3にノイズがかかる場合も同様）。一般に、抵抗値が高いということは小電流でも高い電圧になるということなので、ハイインピーダンス回路はノイズに弱くなる。
まず、受信回路のインピーダンスはある程度高くなくてはならない。極端にローインピーダンスだとショートさせるのと同じことになるし、効率も低下する（効率が低下した分を入力信号の大きさで補おうとすると、シャレにならない大電流が流れる：オーディオ機器の中でもスピーカなどはかなりインピーダンスが低く、PA用のものなどは大電流を扱うので注意が必要）。また送信回路と受信回路のインピーダンスが一致すると効率が最大になるが、そのような接続が可能な回路ばかりとは限らない（受信回路のインピーダンスをもっと高くしないといけない場合もある）。
送信回路のインピーダンスを低く、受信回路のインピーダンスを高く設定（いわゆるロー出しハイ受け）すると、効率が犠牲になるものの受信回路には比較的高い電圧がかかるし、定電圧性も得やすい。しかし、極端なハイインピーダンス回路はノイズに弱い。一方、回路全体を極端にローインピーダンスにすると小さな電圧で大電流が流れて周囲や回路自体に悪影響を与えるうえ途中にある導線の抵抗が無視できなくなる（10MΩの回路を10Ωの導線で繋いでもさほど問題ないが、10Ωの回路を10Ωの導線で繋ぐのは大問題）。さらに、上の図でいうR2（受信部分）とR3（電圧計）の抵抗値の差を確保する必要もある。このような事情がいろいろと重なって、設定可能な範囲には自ずと限界がある。また、インピーダンスが高い回路に大電流を流すと、発熱がエラいことになる。
もうちょっと細かい話として、コンデンサ（キャパシタ）を受信回路と並列に入れた例も考えてみる。
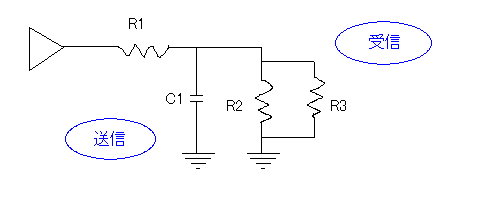
こんな接続はわざわざやらない、と思う人もいるかもしれないが、ケーブルが持つ静電容量（キャパシタとしての性質）などで、意図しなくてもこのような状況は生まれる。上図は「抵抗器とコンデンサを使ったローパスフィルタ」そのもので、1 / (2 * π * R1 * C1) Hzをカットオフ周波数（3db減衰ポイント）として高音が削れる（ハイ落ちになる）。たとえばR1が20KΩでC1が500pFだと、1 / (2 * π * 20000 * 0.0000000005)≒15915なので、だいたい15KHzくらいから上が削れることになる。なお、R1がたとえば1KΩくらいなら、5000pF（こんな大容量が意図せず組み込まれることはまずない）くらいの静電容量があってもカットオフ周波数が30KHz以上になり、音楽用途で普通に使う周波数帯にはまず影響しなくなる（ついでにいえば、インピーダンス不整合による反射波や、抵抗器の構造による特性の乱れも、この周波数帯にはほぼ影響しない）。
以下の傾向は、頭に入れておいた方がよいだろう
ハイインピーダンス：小さな電流でも大きな電圧（高効率）；ノイズに弱い；全体として小電流；ケーブルの静電容量に敏感（ハイ落ちしやすい）
ローインピーダンス：小さな電流はほとんど無視（低効率）；ノイズに強い；全体として大電流；ケーブルの抵抗値に敏感（ヘタをすると燃える）
送信回路のインピーダンスがやむなく高い場合、受信回路との間にパッド（抵抗）を入れて見かけ上の入力インピーダンスを上げる（これは単に減衰させているだけなのでインピーダンスマッチングとは言わない）が、送信回路のインピーダンスが高いということは、微弱な信号を高効率で電気に変換している（たとえばエレキギターのピックアップとか）可能性が高く、パッドが入れられない場合も多い。その場合はトランスを入れるなどしてインピーダンスを変換する（インピーダンス変換により入力インピーダンスと出力インピーダンスを一致させ、効率を最大化することをインピーダンスマッチングという）。ノイズに弱いハイインピーダンス回路の距離を短くするため、送信回路にできるだけ近い場所でインピーダンス変換を行うのが理想的である。
送信回路のインピーダンスが高すぎる場合受信回路との間に抵抗（パッド）を入れてやるということはすでに述べた（送信電流が大きすぎる場合にも同様の対応が可能：ようは送信回路と受信回路の両方に過大な電圧がかからないようにしてやればよい）。図にすると以下のようになる。
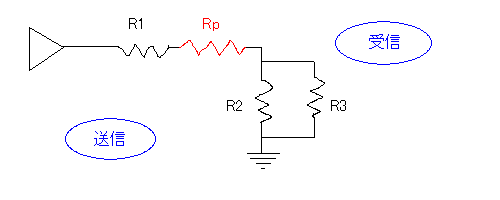
図の赤線の回路がパッド（pad）で、この場合、受信回路の見かけ上のインピーダンスが上がっており、電流の一部がRpで消費されている（その分効率は下がる）。
じつは、インピーダンス（と電流）を調整する方法はもう1つあって、送信回路と受信回路の間でグランドに接続してやってもよい
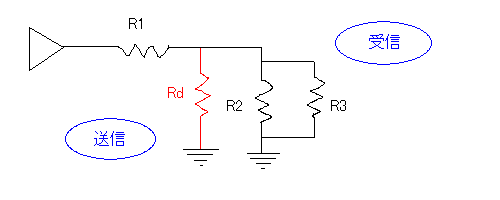
こうすると、電圧が受信回路とRdとに分散される（正確には、直列抵抗R1と残りの並列抵抗で分け合う電圧比が変わる）ため、結果的に受信回路にかかる電圧が下がるのだが、送信回路から見た見かけ上のインピーダンスも下がっている。図の赤線の回路を分圧器（voltage divider/Potential Divider/bleeder）という（Rdをコンデンサに取り替えるとローパスフィルタ、R1をコンデンサに取り替えるハイパスフィルタになる：周波数に依存して分圧の度合いが変わるためで、入れる位置を反対にすればコイルでも実装できる）。Rdで消費される電流とグランドに逃げる電流があるので、やはり効率は下がる（というか、送信回路の起電力は変わっていないわけだから、受信回路にかかる電圧を下げることは効率を下げることと同義である）。
さて、インピーダンスが上がるパッドとインピーダンスが下がる分圧器の2種類を紹介したが、ここで、パッドと分圧器の両方を組み込んでやればインピーダンスを変えずに電流だけを小さくすることができる（つまり、インピーダンスを変えずに効率だけを落とせる）。
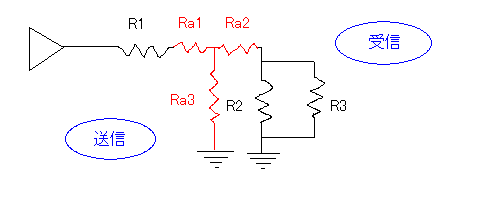
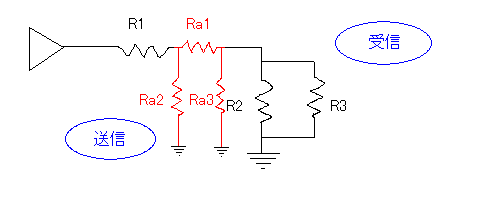
赤線の回路をアッテネーター（減衰器/attenuator/ATT）といい、上のタイプをT型、下のタイプをΠ型という（赤線の部分の形を見たまんまに表現しただけ）。減衰率を定数で与えて連立方程式を作って解けば、任意の減衰率を実現するために必要なRa1～Ra3の抵抗値がわかる（I-Laboratoryというサイトの解説が詳しい）。
本来、インピーダンスを変えずに（あるいは任意のインピーダンスに変更しつつ）減衰だけ行うものをアッテネーターというのだが、オーディオ用語では「高機能なパッド」の意味でアッテネーターと呼ぶ場合がある（英和辞典でも「pad」の訳として「減衰器」が載っている：パッドの方を「減衰用抵抗器」とでも呼ぶべきなのかもしれないが、一般的には狭義のアッテネーターを「定インピーダンス（型）アッテネーター」と呼ぶ）。
英語だとtransformeで日本語だと変成器、変圧器（Voltage converter）と呼ばれることもある。環状の鉄芯（コア：鉄でできているとは限らないが慣例上こう呼ぶ）と環状の導線（コイル）で構成するのが普通。1つの鉄芯にコイルを2セット巻きつけた格好の内鉄型と、2つの鉄芯を1セットのコイルにくぐらせた格好の外鉄型がある（ここで「格好」としているのは、鉄芯＞絶縁＞低圧側コイル＞絶縁＞高圧側コイルと巻くことが多いため：漏れ磁束を減らしつつ絶縁を合理化するため）。
単純な実装としては、トロイダルコア（Toroidal Core：リングコアとも）にコイルを巻きつける方法がある。ぶっちゃけ、鉄の輪っかにガムテープかなにかを巻いて絶縁し、導線を巻きつければトランスになる。
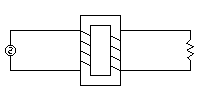
単相なら、外部からの電圧で電流が流れるコイルが1次側、電磁誘導によって電流が流れるコイルが2次側だと思ってよいはず。
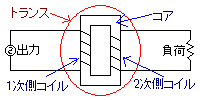
1次側と2次側の相互作用は（絶縁が有効に機能している限り）磁束によるもので、電気的には切り離されている。また、1次側に直流を流しても2次側には作用が生じない。
ここで1次側と2次側のコイルの巻数を変えてやると、出力から見た負荷のインピーダンスが変化する。理想的な回路（損失ゼロで、コアやコイルはまったく等質な素材）を想定すると、1次側と2次側では磁束を共有しており、同じ磁束に対応する電圧は巻数に比例するので、巻数比＝電圧比になる（用語として、変圧前と変圧後の電圧比を変圧比、電流比を変流比という）。
無損失なら1次側と2次側で仕事率（というかエネルギーの総量）は変わらないため、電圧がn倍になれば電流は1/n倍になり、インピーダンス＝電圧を電流で除したものと捉えるとn/(1/n)倍すなわちn^2倍になっていることがわかる。たとえば1次側が巻数1000で2次側が巻数100（＝巻数比10）、1次側の電圧が20Vで電流が0.1Aだとすると、2次側の電圧は2Vで電流は1A、1次側のインピーダンス200Ωに対して2次側のインピーダンスは2Ωになる。
出力から見ると、直接の仕事相手は1次側コイルなのだが、仕事の総量は変わらないままトランスで電圧10分の1の電流10倍に変換され、最終的には2次側コイルが負荷に仕事をする形になる。この回路を出力から見ると、大電圧をかけても小電流しか流れない＝負荷のインピーダンスが100倍になったのと同じである（負荷から見ると、出力のインピーダンスが100分の1になったように見える）。
この原理は、インピーダンスマッチング（出力のインピーダンスと負荷のインピーダンスを見かけ上等しくする：無変調のオーディオ信号ならロー出しハイ受けでも問題ないが、高周波を扱う場合には重要）や、次の項で紹介するバランス変換などに用いられる。
バランスというのは「2つの信号路の釣り合いが取れる＝和がゼロになる」という意味。トランスを使うと多分こんな感じ（想像図なので信用しないように）。
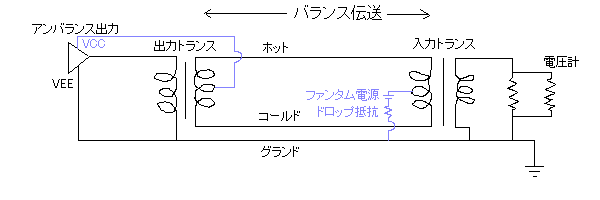
ファンタムをかける場合（図の青線部分）は入力トランスの2次側（左側）に電圧をかけて、出力トランスの2次側（右側）で取り出す（ドロップ抵抗の位置が変だがあまり気にしないで欲しい：3.4kΩを噛ますのが普通らしい）。
オペアンプを使う場合についてはNegibozu's Homepageというサイトにすばらしい回路図があるのでそちらを参照（ただし「ここに掲載する資料はあくまで個人的な覚え書きですので、誤りや不正確な部分があるかも知れません」とあるので記述の正確性は各自が確認すること）。
ダイナミックマイクの場合はボイスコイルの中点をグランドにするパターンもあるらしい。
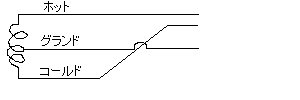
この場合、ファンタム電流やプラグインパワー電流が流れると面倒なことになりそう。
なお、バランス伝送にすることでキャンセルできるのは「ホットとコールドにコモンモードで入ったノイズ」だけで、グランドラインから入ってくるノイズ（とくにグランドがシールドを兼ねる場合や、大きなグランドループがある場合に重要）をアースで逃がさなくてはならないのはアンバランスと同じ。
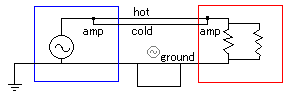
上記はオーディオの重箱の隅で使ったグランドループのある回路図の再掲（トランスではなくオペアンプを使う前提）だが、バランスで送るからといってアースが不要になるわけではないということがわかるだろう。
トランス式のバランスならこんな感じの伝送（グランドリフト：回路としては1:1フロート型の強制バランと同等、なのかな、多分）もできなくはないのだが、
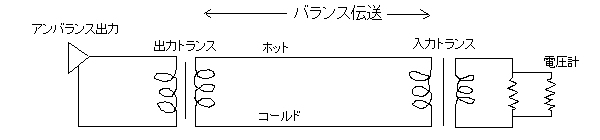
これだと1次側回路が作るループ由来or各種能動素子がグランドに捨てるはずのノイズに逃げ場がないので、グランドの扱いが変な機器がある場合の緊急手段として以外は、あまり有効でない（マトモなアースを取る方がずっとよい）。バランス受けのバランス出しなら、グランド由来ノイズの対策として有効な場合がある（トランスを通す損失とのトレードオフ）。また、すでに他の経路でグランドが繋がっている場合、ループを作らないようにリフトすることは普通にある。
ちょっと変わったところで「コールドを出力インピーダンスと同じ抵抗を介してグランドに落とす」手法もあり「インピーダンスバランス」と呼ばれることが多い（2011年4月現在、TASCAMやdbxなどは「擬似バランス」と称している）。
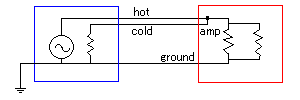
単純にコールドをグランドに落とす（ショートさせる）のとなにが違うのかというと、この接続は「コールドにホットと同じノイズを乗せる」ことを意図したもの、つまりホットが「シグナル＋外来ノイズ」でコールドが「外来ノイズのみ」になれば引き算でシグナルだけが取り出せますね、というプランである（ホットとコールドがバランスしておらず、実際にはアンバランス出力をバランス入力で受けるためのワークアラウンドの1つに過ぎないが、単純な出力回路でバランス伝送のメリットをある程度得られる：なお、単純なショートと同様コールドが信号を担当していないためゲインが半分になり、受信機器側の最大入力は使い切れない）。
コンデンサ（キャパシタ）の使い方と名前。このような回路に組み込んで「交流だけ通して直流を通さない」という性質を利用する。
コイルと違って周りに磁気ノイズをばら撒かないため使いやすい。
まずは並列に入れて交流をグランドに落とすデカップリング（結合防止）コンデンサ。
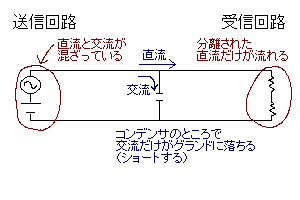
直流電源回路がノイズとして交流成分を出している場合などに使う（出ていなさそうでも普通は念のために入れる）。交流を阻止するので結合防止（正確にはACデカップリングコンデンサだが、単にデカップリングといえば普通これを指す）。上図のコンデンサをコイルに取り替えると直流成分だけ落とせる。
直列に入れるカップリング（結合）コンデンサ。
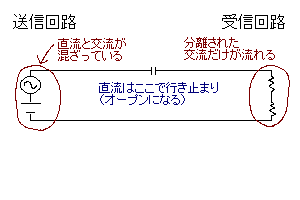
交流信号に直流ノイズ（DCオフセット）が乗っている場合に使う（これも正確にはACカップリングコンデンサで、DCデカップリングコンデンサと呼んでも差し支えない：が、AC回路を扱っていることが明らかなときは普通単にカップリングコンデンサと呼ぶ）。上図のコンデンサをコイルに取り替えると交流成分だけ止められる（チョークコイル/塞流コイル：交流信号から高周波成分を除去するのに使うことが多い）。
回路の一部に並列に入れるバイパス（側路）コンデンサ。
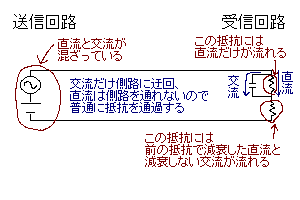
デカップリングコンデンサと似ているが、交流成分が単純にグランドに落ちるわけではない（他の部分で抵抗も通る）のが相違点。コンデンサの容量を小さくすると、周波数の高い成分だけバイパスさせて周波数の低い成分は減衰させることも可能。パスコンと略される。
なお、コンデンサを（単に「導体で不導体を挟んだ素子」ではなく）「電荷を蓄える導体の対」と捉えると、孤立した導体も面積に比例した静電容量を持つことになり、1m^2あたり8.8pFくらいになる（はず）。これは多分「導体は帯電する」ということと同義である、と思う（東京学芸大学基礎自然科学講座理科教育分野松浦研究室による初歩のサイエンスというサイトの解説が詳しいので、ちゃんとした情報はそちらで得て欲しい）。
また「オンorオフに切り替わる直前のスイッチ」や「高い抵抗を挟んだ導線（とくにプリント基板上のもの）」や「2P以上のケーブル」などもコンデンサとして振る舞う。人体の静電容量は100pF前後のオーダーらしい。
リニアPCM（音圧を縦軸に、時間を横軸に取った2次元データ）を前提に。
当たり前だが、録音レベルが過小だとダイナミックレンジに損失が出る。たとえば、規格上のダイナミックレンジが90dbのデジタルオーディオでピークレベルが-8dbの音声を録音すると、最小音と最大音の比は差し引きで82dbになる。
また、デジタルオーディオに増幅をかけると端数の丸め誤差（最大で±0.5）が出る。たとえば縦軸を-127～127までの整数で表現している（＝8bit精度の）データに対し10dbの増幅（3.16倍の増幅と同義）をかけると、1の信号は3に、2の信号は6に、3の信号は9に、4の信号は13に・・・10の信号は32に・・・と、いびつな対応になる（この歪みをディザという技術（別の項で後述）で均してホワイトノイズ（またはそれに近いノイズ）に置き換えることがある）。
マイナスの増幅をかけた場合もダイナミックレンジに損失が出る。たとえば1/2倍（-6.02db）の増幅なら、1～2の信号は1に、3～4の信号は2に、5～6の信号は3に・・・と変換されるので、変換後の信号を見てもそれがもともといくつの信号であったのか判別できない（この場合6.02dbの損失が出ている）。
ダイナミックレンジを圧縮すると、音圧の高い部分で情報の損失が出る。たとえば、縦軸を-127～127までの整数で表現しているデータに対し-12db（音圧の値で言うと32）を閾値に1/2の圧縮をかけた場合、圧縮の対象となったデータについて、元の数値が32よりもいくつ大きかったかという情報が1bit分失われる（ただし、音圧が高いので小さな差異は聴覚上あまり問題にならないが）。
これに加えて、ダイナミックレンジを圧縮した後は増幅をかけるのが普通なので、前述のとおり最大で±0.5の歪みが出ることになる。
結局何が言いたいのかというと「デジタルデータも加工すれば劣化する」ということ。それぞれの操作がどういった劣化をもたらすのかをある程度把握しておけば、より効率よく作業できる。
データ変換にさえ気を使えば、編集作業を最終的な産物よりも高い精度のデータで行う（たとえば、24bit精度のデータで編集して、16bitのCDデータを作る）のも有効で、とくに微小な音の劣化を防ぐ効果がある（Aucacityでは32bitでデータを扱うのが標準になっている）。
また、デジタルイコライザなど、FFT（高速フーリエ変換：離散フーリエ変換(DFT)を高速に計算する手法で、計算結果はDFTと一致する）を用いたものにも誤差がある（詳しく解説しているサイトがあるので、興味がある人はそちらを参照：トップページ）。データレベルの損失もさることながら、聴覚上の変化（アタックが弱くなる）もあるので十分注意する。
数値Nを「N＝±(小数×基数^指数)」で表そうとするもので、2進数での実装上は「N＝(-1)^Sign×2^(Exp＋ExcessN)×1.Fraction」という形になる（イタリックの文字列には、それぞれデータの値が代入される：この形に直すことを「（浮動小数点数の）正規化」といい、正規化可能な数を正規化数という）。Exp（Exponent）の部分を指数部、Fractionの部分を仮数部と呼ぶことがある。
IEEE754の単精度浮動小数点数（Single Precision Floating Point：32bit）だと、Signは1ビット、Expは8ビット、Fractionは23ビットの2進数（プラス「1.」の部分で都合24bit：これを「暗黙の整数ビット」とか「implicit」という）で表現され、ExcessN（データによらず、フォーマットにより決まる）は-127（2進数で-01111111）になる。
どういうことかというと、2進数ビット列「01000000101000000000000000000000」（16進数表示だと「40A00000」）が「0 10000001 01000000000000000000000」に分割され「N＝(-1)^0×10^(10000001−01111111)×1.01000000000000000000000＝(-1)^0×10^10×1.01」と解釈される。10進数に置き換えると「N＝(-1)^0×2^(129−127)×1.25＝1×2^2×1.25＝5」だとわかる。
ビット数を稼ぐためにFractionの整数部分を「1.」に固定しており、これだとゼロが表現できないが、ゼロは「00000000000000000000000000000000」で表現している。上の公式に当てはめると「N＝1×2^-127×1＝2^-127」だが、Expが「00000000」のパターンと「11111111」のパターンは、ゼロ・無限大・非正規化数（Denormal Number/Denormalized Number/Subnormal Number：指数部分の桁が不足して小数部分が「1.～」ではなく「0.～」になるような、絶対値が非常に小さい数）・非数（Not a Numberの略でNaNと呼ぶ：0による除算や負の数の平方根など、数（あるいは実数）でない値を要求すると返ってくるものだが、現実的にはエラー通知である）のために予約されている。
なお、上記（またはそれに近い）フォーマットの浮動小数点数を「単精度」として、それよりも細かい表現が可能なもの（一般には、ビット数を倍に増やしたもの）を「倍精度」と呼ぶことがある（追加したビットをExpに振り分けるかFractionに振り分けるかはフォーマット策定者の任意で、また名前は「倍」精度でも実際の有効桁数が倍とは限らない：たとえばIEEE754の単精度浮動小数点数は10進数で7桁程度、倍精度浮動小数点数は10進数で16桁程度になるようだ）。
リニアでない、と漠然と書いたが、どういうことか。たとえば整数の場合、ある整数とその次に大きい整数との差は常に「1」で、3と4の間も1ならば5678と5679の間も1である。浮動小数点数の場合「0 10000001 01000000000000000000000（10進数で5）」の次に大きいのは0 10000001 01000000000000000000001（10進数で5.00000032）」だが、「0 10000010 01000000000000000000000（10進数で10）」の次に大きいのは0 10000010 01000000000000000000001（10進数で10.00000064）」になる。
ようするに、Expの値が1大きくなるたびに最小の変化幅も2倍になるということなのだが、これは「絶対値が小さいと変化幅が小さく、絶対値が大きいと変化幅が大きい」ということである（変化幅が大きいとはいっても、0db FSに対する相対的な変化幅は、最大でも整数部分のビット深度をリニアPCMで使った場合と（暗黙のビットがあるため完全に同一視はできないが）同等）。浮動小数点数の本質は、小数表現よりも指数表現にあると見た方がよいのだろう。
これは音波をPCMとして記録する際に都合がよく、ダイナミックレンジを大きく取れる。というか、まったく無意味なほど大きく取れるので、余ったダイナミックレンジをヘッドマージン（的なもの）などに流用しているようだ（「WAVE_FORMAT_IEEE_FLOAT」「IEEE_FLOAT」「Microsoft 32 bit float format」などと呼ばれるフォーマットが主流らしいが、具体的な仕様は見つけられなかった：Audacity1.26が出力するWaveファイルではデシマルで-1と1が0dbFSに相当しており、表現範囲を単純に使い切れるのだとすれば、770dbちょっとのヘッドマージンになる）。
ただし、リニアPCMとのデータ互換性には難点があって、整数＜＞浮動小数点の変換はロスレスでない（実用上の不利益はない）。
まず、単純に計算速度の面で整数演算や固定小数点数演算よりも不利である。ただし、最近のCPUは浮動小数点演算用に専用のコプロセッサを搭載しているものがほとんどで、ハード性能によるカバーが可能になっている。
もう1つの面倒さは誤差によるものである。どれも微細な誤差なのでオーディオ用のPCMデータにはあまり関わりがないが、厳密な正確さを求められる計算や誤差が累積する計算などでは大きな問題になることがある。
大まかに分けるとこの誤差には2種類あって、数値の表現法によるものと概数の演算によるものがある。前者は、無理数や循環小数をある程度の有効桁数で近似しなければならないという事情による。1/3や√2などの他、0.05など小数の一部や絶対値が非常に大きい整数の一部なども近似でしか表現できない（丸め誤差・打切誤差など）。後者は、概数同士の演算時に有効桁数が大きく減ってしまう現象。5^100＋7^-100など、絶対値の差が大きい数での加減算や、√100001−√100000など、演算結果の絶対値が小さくなる数での加減算で発生する（桁落ち・欠落など）。
主に電気通信に用いる変調の話。変調方式について、たとえば「FM」は「Frequency Modulation」の略なので「FM変調」などと呼ぶのはちょっとおかしいのだが、以下では便宜上「変調」をつけて記述する。
信号をそのまま電気信号に変換しただけのものを通信に用いようと思うと、弱い信号が埋もれてしまったり、通信経路のf特によって信号が変化したり、必要以上に周波数帯を消費してしまったり、通信に適した周波数域が使えなかったりする。
たとえば20Hz～20KHzでダイナミックレンジが60dbの音声信号の場合、これをそのまま電波にして飛ばそうと思うと、20Hz～20KHzの周波数帯を丸々消費してしまうし、20Hzなどという低周波（電波分類でいうと極極超長波に相当）は一般的な電波通信に適さないし、最小音がノイズに埋もれないレベルを確保しつつ1000倍（60db）の強さで最大音を送ってしまうと効率が悪い。
ということで、なにか一定の信号（サイン波を使うことが多いが、矩形波やパルス波や三角波なども使われる）に変化を与えて、その変化の様子によって信号を伝える手段が発明された。ここで、媒介となる一定の波を搬送波（キャリア）、実際に伝えたい波を信号波（シグナル）、変調後の信号を変調波という。
信号の強さ（振幅）に変調をかける。Sを信号波、Cを搬送波、Aを変調波、Sの最大振幅をプラスマイナス1とすると、A＝（1＋S）Cとなる（なお、単純にSとVの積を取るものはリング変調と呼ばれ、変調波をRとするとR＝SCになる：このような処理をヘテロダインまたはヘテロダイニングと呼び、sin(x) * sin(y) = {cos(x - y) - cos(x + y)} / 2 なので、バンドパスフィルタを使って必要な方を取り出す（右辺の片方が無視できるようにする）と「周波数の平行移動」ができる）。
サイン波を搬送波として用意し、
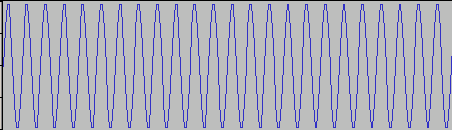
AM変調をかけて（適当に作業したので波形としては変だが、まあ気にせず）たとえばこんな波形にすると
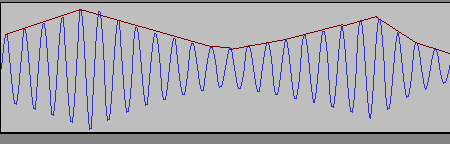
赤線で示した波形が信号波となる。ちなみに上図で、信号波がなす曲線（赤）は変調波がなすすべての曲線に接している（＝共通接戦を持つ）が、このような曲線を包絡線（envelope：音量の経時変化を示すエンベロープとは別の概念）と呼び、変調波の包絡線を取り出すことを包絡線検波と呼ぶことがある（ここでいう検波は復調、つまり変調の反対の作業を指す）。
概念としては上記のようなものだが実装上、元の波形をプッシュプル回路に通して、途中でリング変調し、合算してから送信し、受信したらローパスに通す形も考えられる。
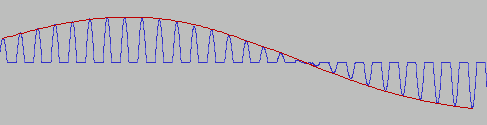
図ではキャリアが半波整流したサイン波だが、全波整流した方が能率が上がるし、同じことを矩形波でやればPCMにローパスをかけて再生するのと似たような処理になる（これだけ気合を入れて図を作ったのでちょっとキレイ）。
横軸の解像度（デジタルオーディオで言うサンプルレートに相当）は搬送波の周波数によって、縦軸の解像度（ダイナミックレンジ）は搬送波の強さと送受信機の精度によって決まる。単一の周波数のみを使って通信できるのが特徴。
信号の周波数に変調をかける。
波形は省略するが、低い周波数を受け取るとマイナスの電流、高い周波数を受け取るとプラスの電流（逆でも構わないが）を流す装置を受信機にすればよい。
サンプルレートは送受信機の精度によって、ダイナミックレンジは利用できる周波数の幅（最低何Hzから最高何Hzまで変調してよいのか）と送受信機の精度によって決まる。常に同じ強さの電波を送信できるため、小さな出力でもダイナミックレンジの広い信号を伝達できる。
この場合、位相（信号の電圧をy=sinθのグラフに見立ててそのθの値：ようするに現在の電圧をピーク電圧で割ったもののアークサインだが、微分しやすいようψ(t)=A*sin(ωt+α)のωt+αの部分と考えてもよい）の変化が速ければ信号波がプラス側、遅ければマイナス側に振れる、つまり位相の変化（ωt）を時間で微分してやると信号波の波形が得られる。
実装上、周波数変調回路（LC発振器にAFC回路でフィードバックを与えて作るらしい：よくわからない）よりも位相変調回路（可変容量ダイオードで作るらしい）の方が簡単に作れることから、直接周波数を操作するのではなく位相を操作してやることが多い（間接FMと呼ばれる）。「位相をどんどん進める」ことと「周波数を高くする」こと、「位相をどんどん遅らせる」ことと「周波数を低くする」ことは結果的に同義なので、信号波の振幅と周波数変化の対応が1次式で表せる場合、理想的な処理を行えばどちらの経路でも出力に違いはない。
数式については次の項で後述するが、位相変化を時間で積分して積分区間で割る（平均を取る）と周波数に、周波数を時間微分すると位相変化になる。正弦波の場合振幅と位相変化速度は常に一定なので、周波数がf(Hz)であることと1秒に2πf(ラジアン)の割合で位相が変化することが同義で、位相変化を時間で積分して初期位相を加味すると現在の音圧になる。
このパートの内容について、筆者は他のパートよりもさらによくわかっていないので、眉に唾をつけて読んで欲しい。
WikipediaJPの記述によると、時間をt、搬送波をVc、搬送波最大値をVcm、搬送波周波数（中心周波数）をfc、信号波をVs、信号波最大値をVsm、信号波周波数をfs、被変調波をVm、被変調波位相角をθm、変調指数（最大周波数偏移を信号波周波数で除したもの）をmとするとき、
Vc = Vcm * cos(ωc * t) = Vcm * cos(2*pi*fc * t)
Vs = Vsm * cos(ωs * t) = Vsm * cos(2*pi*fs * t)
Vm = Vcm * sin(θm)
と書ける。ただしωは角周波数で、ω＝2πfとして扱う。
ここでVmの初期位相をゼロとすると（という前提がどこから来るのかわからないが、その方が計算がラクなのかもしれない）、θmはωmを0からtまで時間積分したものなので、実際に計算して代入すると
Vm = Vcm * sin(ωc * t + m * sin (ωs * t))
が得られる。つまり、Vcの位相をmsinωst変化させてやるとVmが得られるということになる（cosωstを積分するとsinωstになるので、位相をVsの積分（の定数倍）だけ変化させるのとも同義：このためアナログ回路では信号波をローパスフィルタ（＝積分器）に通してから位相変調回路に入力するのが一般的）。
上記は正弦波を前提に考えているはずだが、標本化した実測データ（つまり普通のデジタル音声）に当てはめる場合も、結局は正弦波が複数重なっているだけなので同じ扱いになる（はず）。フーリエ変換してから連続角周波数に別値を代入するのかな、という気がするがよくわからなかった。搬送波が正弦波なら、複素平面上の移動で処理できるらしい。
AMやFMとはちょっと毛色が違い、アナログの電気通信にも使えないことはないが、デジタルデータに適した方式である。
パルス振幅変調（PAM）は、AM変調ないしリング変調の搬送波にパルス波を使うもの。図（いい加減だが）にすると以下のようになる
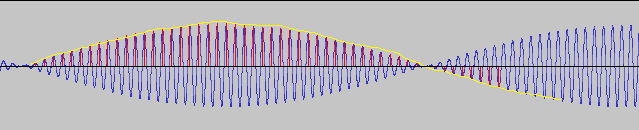
黄色が信号波、青がリング変調した場合の変調波、赤がPAM変調した場合の変調波。信号波を「時間軸方向に切り分けた」（＝標本化した）格好になっているのがわかるだろうか。
ここでさらに、振幅の大きさをデジタル値に変換（量子化）してやると、PCM（Pulse-Code Modulation）データが得られる（搬送波の周波数がサンプリング周波数、振幅データの解像度がビット深度に相当）。このデータはデジタル処理が容易なため、パソコンやオーディオCDなどで幅広く使われている（図でパルス波を使っている部分を矩形波に差し替えてやると、PCMデータから補間なしで生成した波形に一致する）。
パルスの密度を利用するもの（パルス密度変調/PDM/Pulse Density Modulation）もあり、こちらはFM変調の搬送波をパルス波（または1サンプル周期分の矩形波）にしたような感じ。パルスが密であれば電圧が高く、疎であれば電圧が低いと解釈する。
たとえば「0100001000000000100001001011010011101101111110」などというデータがあった場合「0100001000」の部分は1の数が少ないので電圧が低く「1101111110」の部分は1の数が多いので電圧が高いということになる。
これをどうやって処理するかというと、値の総和（Σ）を監視して、その変化量（⊿）を検出してやればよい。すなわち、0が多い個所ではΣがあまり増加せず、⊿Σが小さな値になる一方、1が多い個所ではΣが大きく増加して、⊿Σが大きな値になる（⊿Σ変調という）。逆から説明することになったが、信号波をデータに変換する際は振幅が⊿Σになるような数列を出力してやればよい。
SACDのDSD（Direct Stream Digital）やシャープなどが力を入れている1ビットデジタル技術は、PDMを応用したもの（というか、ほとんどPDMそのもの）らしい。パルス幅変調（PWM/Pulse Width Modulation）というのも似た感じで、こちらは密度の代わりに矩形波の横幅（正確にはデューティー比と呼ばれる）で電圧を表現する。実装としてはたとえば、アナログ信号と搬送波（三角波）をコンパレータ（比較器）に入れて、アナログ信号の方が電圧が高いときにはプラス、低いときにはゼロまたはマイナスの電圧を出力すればよい（オペアンプの動作そのもの）。ローパスフィルタによってアナログ波形を復元できるのはPDMと同じで、D級アンプ（デジタル式の実機アンプ：増幅段はコンパレータとローパスの間に設けるのが普通）などで利用されている。
⊿Σ変調の際、量子化器の前に積分器を入れて、量子化器の出力を積分器の前にネガティブフィードバックすると、量子化器のノイズ（＝量子化ノイズ）だけ微分する（＝ハイパスフィルタにかける）ことができる（ただし、増幅もかかるのでノイズの総量が減るわけではない）。これをノイズシェイピングといい、フィードバックの段数が多ければノイズシェイプも急峻にできるが、高次のものほど安定させるのが難しく、3次以上では発振の可能性があるらしい。これによって、浅いビット深度で高いサンプリング周波数のデータを深いビット深度で低いサンプリング周波数のデータに変換することが容易になる。実装上、たとえば16bit/48KHzの量子化器よりも1bit/3072KHzの量子化器の方が安価で安定するらしく、アナログ信号をノイズシェイピングありの⊿Σ変調でPDMに変換してから、改めてPCMにDD変換する手法が広く利用されている（安直に数列の和でDD変換を行うと、ものすごく高速なサンプリングが必要になってしまう）。
未確認情報だが、64fs1bitのPDMデータ（fsは、周波数1や周波数2などをf1やf2などと書くのと同様の表現で、サンプリング周波数を指す：日本では64fsを64倍オーバーサンプリングと呼ぶことが多い）を1fs16bitのPCMデータに変換できるらしい（おそらく、AD変換＞DD変換までのノイズが16bitPCM本来の量子化ノイズに対して十分小さくなるという意味だと思う）。1bitPDM＞16bitPCMのDD変換をするときに、1bitPDMのサンプルレートは16bitPCMのサンプルレートの64倍あればよい（たとえば、DD変換で44.1KHz/16bitのPCMデータを得たい場合、16bitPCMの性能を活かし切るには、2822.4KHz/1bitのPDMデータがあればよい）ということである。
内部処理NbitによるK倍オーバーサンプリング時にS/Nの理想値が、Straight oversamplingで6.02N+1.76+logK、First-order noise shapingで6.02N+1.76-5.17+30*logK、Second-order noise shapingで6.02N+1.76-12.9+50*logKになるという解説もあり、こちらの方が信憑性が高そうなのだが、Kを10倍にすると1または30または50db、Nを8増やすと48dbのS/N改善になる理屈である（あくまで理想値なので、実際の値とどのくらい開きがあるのかわからないが）。Second-order noise shapingの式にN＝1とK＝64を代入すると約85dbになるから、16bitPCMを得るとき64fs1bitのPDMを使うという話とも整合性があるように思える（同様にN＝1とK＝256を代入すると115dbくらいになり、実用上はこれ以上頑張ってもあまり意味がなさそうに思える）。まぁいづれにせよ、問題は最終的なダイナミックレンジと歪率（もしくはS/N）なので、途中でどう処理しているかは深く考えなくてもよいだろう。
フーリエ解析を行うには無限区間の積分が必要だが、実際のデータは有限なので、無限にループしているとみなして積分する（つまり、終端と始端を貼り合わせてデータを引き伸ばす）。ここで、始端と終端をただ貼り合わせただけではフーリエ解析ができない（筆者はこの理屈をほとんど理解していないが、終端から始端にループしたときに数値が飛び跳ねたらまずいだろうなということは想像できる）。
そこで、両端が0になるような関数を掛け算してから解析するのだが、このとき掛け算する関数が窓関数（時間関数/時間窓）で、1ループ分に含まれるデータの数がサンプル数。窓関数を掛け算することを「切り出す」と表現することがある。また、窓関数自体も波動関数である（0から始まってまた0に戻る連続した関数だから、ループさせてつなげれば波動になる）。
ここで、できる限りなめらかにつなごうと思うと、なだらかな山状の窓関数を使うことになるが、そうすると波形が潰れる範囲が広くなり、結果的に周波数の分解能（精度）が落ちる。端だけを急激に落とせば潰れる範囲は狭く、たくさんのサンプルが「生きる」ので分解能は上がるが、つなぎ部分にノイズが入るため小さな信号は埋もれてしまう。
このバランスを知るために、窓関数のスペクトラム（サイン波を窓関数で切り出して、フーリエ解析したもの、だと思う）を利用するのだが、縦軸に強さ、横軸に周波数を取ったグラフにすると、真ん中に一番高い山がある山脈のような形になる。ここで、一番高い山をメインローブ（main-lobe）、その他の低い山をサイドローブ（side-lobe）というのだが、メインローブの幅が狭いほど分解能が高く、サイドローブの高さが低いほどノイズが少なくなる（詳細な解説をしているサイトがあるので、知りたい人はそちらを参照：参考1、参考2）。
近似データであるから、サンプル数が多ければ多いほど精度（分解能）は上がる。計算の手間は、サンプル数が多くなるにしたがって線形対数オーダーで増える（n*log(n)のオーダー：nが十分大きい場合、n個のサンプルに対する計算量と比較して、n^2個のサンプルに対する計算量は2n倍になる）。また、当然だが、測定可能な最低周波数はサンプル数に依存する。
ただし、フーリエ解析というのは「特定時間帯の平均値」を求める作業なので、サンプル採取範囲内で周波数成分の変化があると困ったことになる（スイープ信号を処理する場合などにとくに問題になる）。音声用のスペアナとして使う場合、サンプル数は周波数変化が無視できるくらい小さくなるように設定すべきだろう。ちなみに、Audacityのスペクトル表示は指定サンプル数のフーリエ解析を指定範囲の終わりまで順次行って、結果の相加平均を表示するようである（バージョン1.2.6現在、1048576（＝2^20）サンプルまで選択でき、44.1KHzだと最大23.8秒になる：指定サンプル数に満たない端数は、末尾のサンプルを切り捨てているようだ）。リアルタイムでスペクトラム分析をする場合も、サンプル数が多いと信号の変化に対する追従性が悪くなる（信号が変化しているのに、いつまでも古いデータの影響が残ることになる）。
反対に、データの時間変化がゆっくりであれば、サンプル数を増やすことで窓関数による分解能の低下を補うことができる。たとえば、あるサンプル数での方形窓による分析と、サンプル数を√2倍（1.41倍）にしたハニング窓による分析は同じ精度になる（はず、多分）。また、全体のサンプル数に対しノイズが乗るサンプルが減るため、ノイズの影響も少なくなる。
440Hzのサイン波を最低音として、その倍音を-6db/octの勾配で4オクターブ分重ねたサンプルを解析した（周波数は440・880・1760・3520Hz）。山の明確さが精度を、谷の深さがノイズの少なさを示しているが、周波数を対数表示（薄い青紫の縦格子1本で1オクターブ）しているので、高域ほど横幅が縮んで表示されていることに注意。
周波数について言えば低域ほど小さな誤差にも敏感だということで、サンプル数が同じであれば測定精度自体は同じである（たとえば16KHzを測定する場合なら上下10Hz程度の誤差はほとんど問題にならないが、16Hzを測定する場合はそうはいかず、低域ほど「音程」を知るために高い精度を要求するということ）。
ピーク周辺のノイズについても、低音側でノイズが増えているのは似通った周波数の音が密集している（今回の例でいうと、440Hzと880Hzの間は440Hzであるが、1760Hzと3520Hzの間は1760Hzで、間隔が4倍も違う）ためで、同じ音圧のサイン波であれば、周波数に関わらず同じようなサイドローブになる。
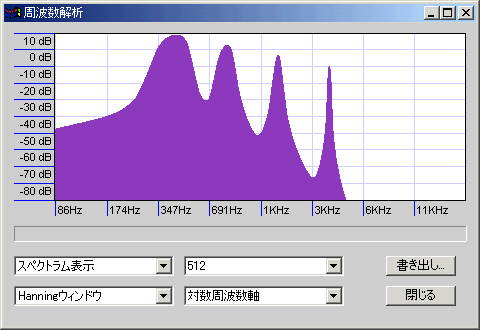
低音はかなりぼやけているがノイズは少ない。
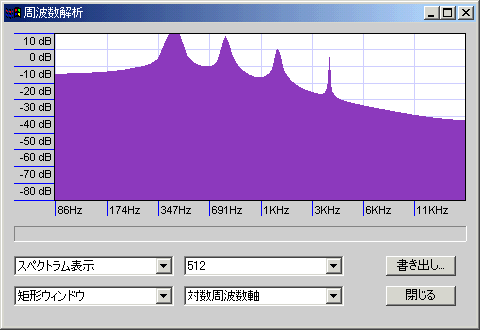
低音も解析できているがノイズ山盛り
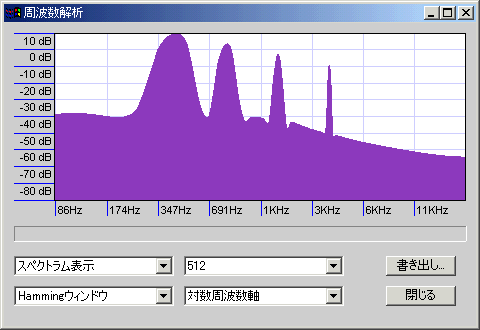
上2つの中間くらい
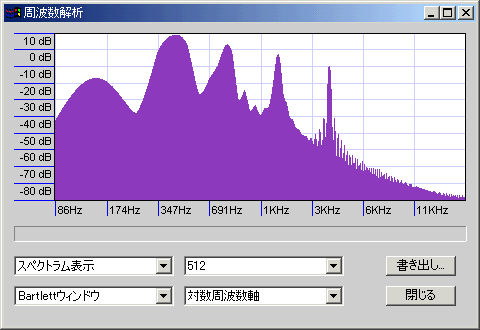
Hammingより精度が高くノイズも少ないようだが、ノイズの乗り方が変。
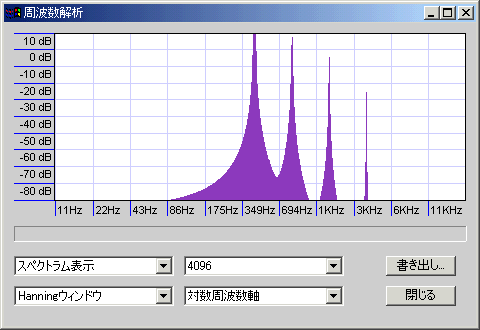
このくらいのサンプル数を取ってやればHanningでもスッパリ
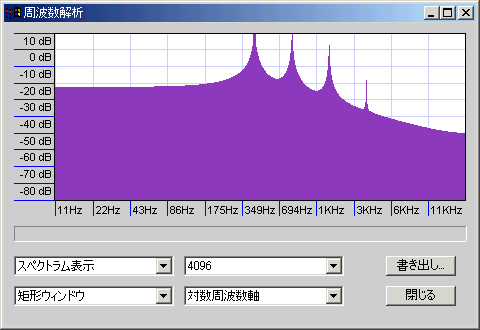
ノイズが減っている
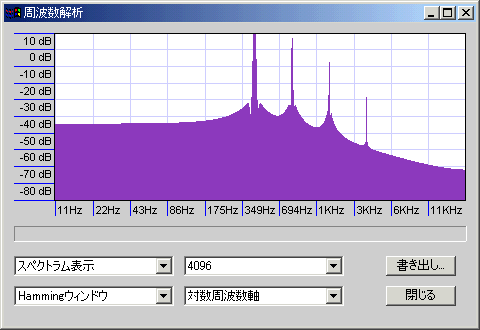
相変わらず中間的な特性
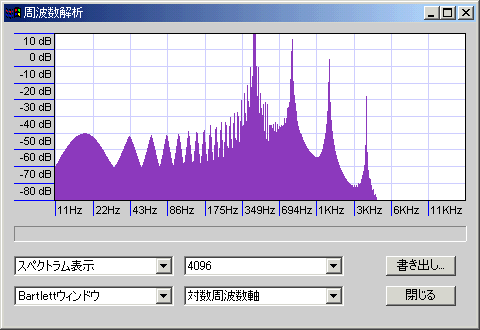
相変わらず変なノイズ
とりあえずHanning窓を使っておいて、周波数がぼやけて困るようならHamming窓や方形窓に切り替える、という使い方が便利だと思う。
声の音色によってスペクトラムも当然変わってくるが、その大まかな特徴を紹介。
以下すべて筆者の声を分析したもの（録音したままで無加工：環境ノイズはピンクノイズに近く、解析の都合で非常に低い周波数が実際よりも盛り上がって見える）だが、なんとなく気恥ずかしいので音声ファイルはなし（ヴォーカルトレーニングのCDなどを買ってくれば、ちゃんとしたプロのデモンストレーションが録音されている）。発音はすべて「ma」でビブラートなし、エンベロープでいうサステインの部分のみを測定した。
オペラっぽい声。
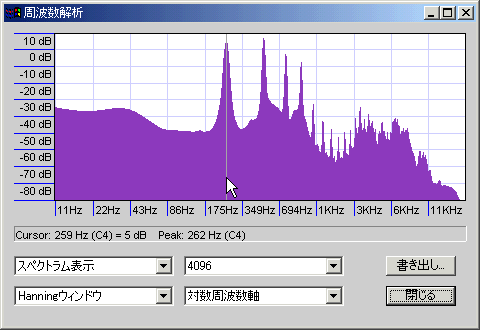
偶数倍音が豊富で、高次倍音はやや弱め。
ハスキーボイス。
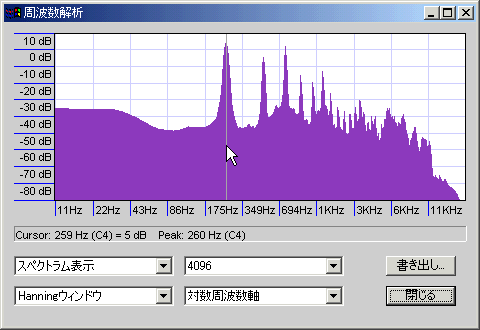
5度上に当たる倍音が豊富で、高次倍音も減衰が少ない。
捻り出す感じのハイトーン。
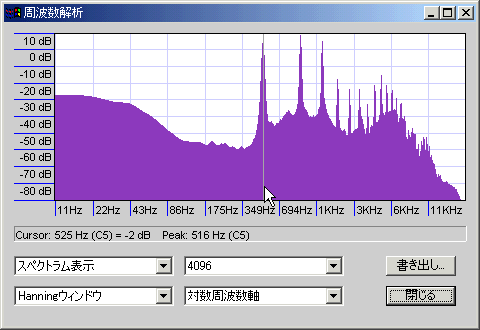
2倍音と3倍音が両方くっきり出ており、高次倍音も減衰が少ない。もうちょっと声量を大きくしないとそれっぽい形にならないか。
完全な裏声。
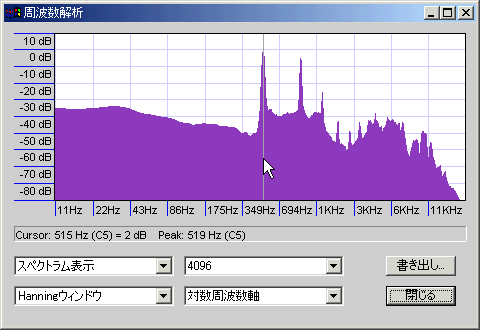
音が非常に薄い。
オペラっぽい声（声量大）。
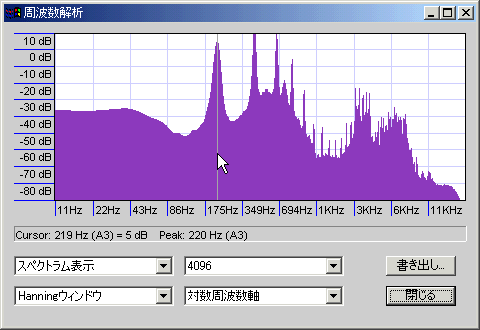
やはり偶数倍音が豊富で、3倍音もそこそこ、高次倍音は弱め。
捻り出す感じのハイトーン（声量大）。
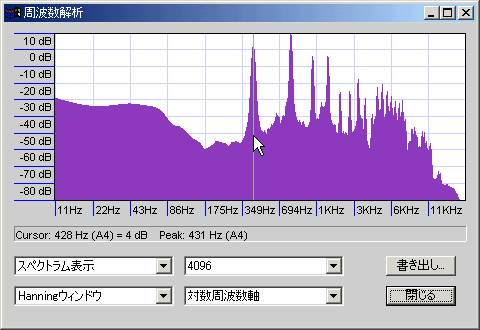
2倍音が強く、以後も減衰少なく上まで続く。ベースの上にハスキーボイスが乗ったような形。
かすれた感じのややハスキーな声。
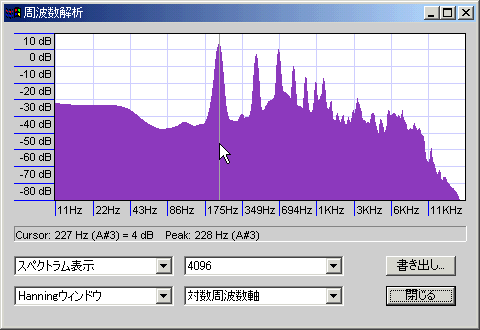
普通のハスキーボイスと似ているが、谷が低くならない（音程が不明瞭というか、いろいろな周波数の音が入り混じっている：結果的にホワイトノイズが乗ったようなグラフになる）のが特徴。6倍音も少なめ。
透明感を意識したややハスキーな声。
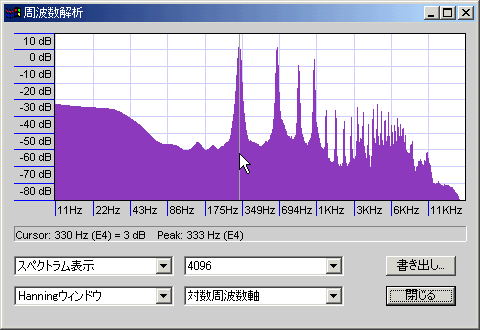
1・2倍音と3・4倍音とそれ以降が、わりと行儀よく並んでいる。谷が深いのが特徴。
地声。
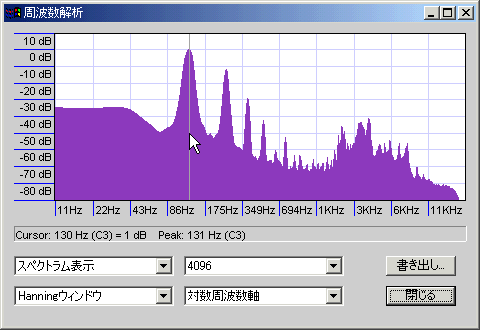
普通。3KHz周辺が持ち上がっているのはマイクの特性っぽい。
ホーメイ（ホーミー）もどき。
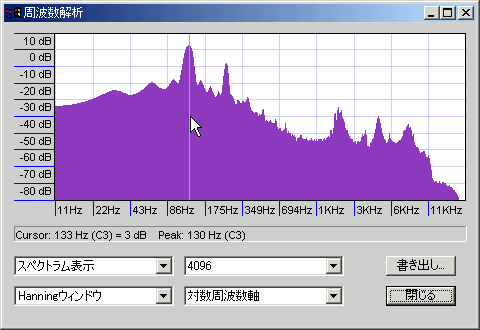
口の中で音を潰しているだけの疑似ホーメイなので、本物とは形が違う（多分）。倍音がほとんど目立たず、低音ノイズの上に1倍音と2倍音がオクターブで重なっている格好。
ややかすれた、力の抜けた声。
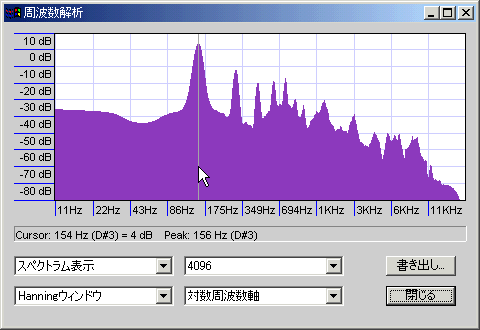
3～5倍音が特徴的。
ヴォーカリストの人は、ぜひ1度自分の声をスペアナにかけてみることをオススメする（Audacityのようなノンリニアのスペアナではなく、リアルタイムのスペアナがよい：efuさんのWaveSpectraというソフトが非常に高性能）。自分の声の成分を知ることで、アレンジャーへのリクエストも出しやすくなるし、ボイストレーニングにも使えるだろう。また、「自分の声」をスペクトルとして覚えておくと、普段と違う機材を使う場合に補正的なイコライズをかけやすい。
PAをやる場合、イコライズでかなり声のキャラクターを変えられるということを覚えておくとよい（次の項目で触れるフォルマントの問題もあるので簡単ではないが）。アレンジャーの人は、ヴォーカリストの音域を把握して他の音とのぶつかり具合を把握する。シンセでコーラスボイスなどの音色を作る場合も、編集の指針としてかなり使えるはず。
ヴォーカルのスペクトラムは、音色の決定だけでなくことばの判別にも関わっている。声のスペクトラムのピーク部分をフォルマント（ホルマント）と呼び、低音側からF1、F2、F3などと表記する。基音の倍音成分に当たるフォルマントを移動フォルマント（基音のピッチが変わるとそれにともなって移動するから）、それ以外のフォルマントを固定フォルマントというが、これらが複合して音のキャラクターを作っているのだと思われる。
専門的な話は沖電気のウェブサイトにある声の種類と発声のしくみというページが詳しいが、通常会話では200～1000Hz周辺のF1と1500～3000HzのF2の関係で母音をほぼ特定できる。逆にいうと、F1とF2の関係が崩れるとことばが聴き取れなくなるので、この周辺にイコライザをかけるときは注意しよう。
筆者の声（基音117Hz）で試してみたところ、3KHz周辺を削るとエの音が、2KHz周辺を削るとイとエの音が、1KHz周辺を削るとアとエの音が判別しにくくなった。とくに、2KHz周辺を削ったときのエの音はほとんどわからない。高い声（基音335Hz）で試してみても2KHz周辺を削ると聴き取りにくかったので、エの判別は固定フォルマントが強く関わっているのかもしれない（実際のところは不明）。2KHz周辺を持ち上げるとやはりエの音が聴き取りにくくなったが、削ったときほどではなかった。ちなみに人間の声は、基音880Hz程度が最高音（ソプラノの場合）。
Yamamoto's Laboratoryというサイトの解説やスズメレンダラー開発日記というサイトの解説の方がはるかに高精度なので、詳しく知りたい人はそちらを参照。
デジタル（離散）データをアナログ（連続）データに変換する場合など、サンプルとサンプルの間がどのように変化したかを推測する必要があるが、この推測作業を補間（Interpolation：サンプルの範囲外を推定するのは補外）という（内挿/外挿という表現もよく見られる）。PCMデータの場合、時間を横（x）軸、音圧を縦（y）軸に取った平面図形上で処理するのが普通である。
たとえば、音圧が「1、5、4、2、-2、1」などと変化するデジタル音声があった場合、1と5の間は2と3と4を通って5になったはずだが、それがどのような経過を辿ったのかを推測する。
いちばん簡単な方法は、値を飛び飛びに変えてしまう方法である。上記の例なら、たとえばAとBの間はずっと音圧1、BとCの間はずっと音圧5、といった具合である。
計算量がほぼゼロに近いため処理が高速（とくに実効値を近似値で求める演算は、単純な足し算で済むため非常に速い）ではあるが、デジタル音声の説明でよく出てくるような階段状の波形になってしまう（PCMデータを矩形波の集合としてみるとこのような波形になる）。
自然界の音を録音したデータであれば、そのようなカクカクした音が入っている可能性はほとんどないため、これは原音に忠実な波形とはいえない（音質でいうと、高音ノイズが目立つということになる：ここでいう高周波ノイズは量子化ノイズやサンプリングノイズ（どちらもホワイトノイズ分布：変調ノイズをサンプリングノイズに含めるなら、ピンクノイズの逆勾配になったりもするが、いずれにせよそう複雑な分布にはならないのが普通）とは別のものである）。
次に簡単な方法は、それぞれのサンプルを直線で結んでしまう方法である。上記の例なら、座標A（0, 1）、B（1, 5）、C（2 ,4）、D（3, 2）、E（4, -2）、F（5, 1）を順に直線で結び、その方程式を求めればサンプルとサンプルの間を推定できる。たとえばBとAの間はy = 4x + 1の方程式に従うため、時間0.5における音圧は3、時間0.25における音圧は2だったと推定できる。
この方法を1次補間（線形補間とも）といい、計算は非常に楽であるが、できあがる波形は（補間なしよりはマシだろうが）やはりカクカクとしたものになる。補間なしよりは処理が重いものの、かなり高速でそれなりに元波形の雰囲気も伝えられるため、波形表示に適している（波形編集ソフトで音圧グラフを表示すると、たいてい線形補間で表示されるが、音を再生したときには別の方法で改めて補間されるのが普通）。
台形公式で数値積分の近似解を求めるのもやっていることは同じ（線形補間して積分するのと台形公式を使うのは同義）で、長めの区間で合計値が問題になるような場合はそこそこの精度になる。
そこで、もっとなめらかにサンプル同士をつなぐ方法を考える。線を丸くしたいのだから、1次式（直線）ではなく多項式（曲線）にしてやればよい。上記の例なら、（0, 1）、（1, 5）、（2 ,4）、（3, 2）、（4, -2）、（5, 1）の6点を通る曲線の方程式（5次）を求めてやる。
ラグランジュ補間と呼ばれる方法で、1次補間と違い、サンプル数が増えると計算量が爆発的に増える。また、サンプル数が多い（方程式の次数が高い）と、グラフが「暴れる（大きな誤差が出る）」傾向がある（ルンゲの現象）ため、普通は3次式を使う（ので3次補間とも呼ばれる：そうすると5点以上のサンプルを補間できないわけだが、後述の繰り返し手法で解決する）。
たとえばシンプソンの公式では、2次のラグランジュ補間を利用して数値積分の近似解を求める。また、ラグランジュ補間に「重み」を付加して精度を上げることもある（ここでいう精度は積分値のことで、具体的には音圧の実効値が原波形の実効値により近くなる：重みの付け方によってニュートン・コーツ型やチェビシェフ型やガウス型などがある）。
上記を少し応用して、少数（普通は2つ）のサンプル同士を次々に、たとえば、点AとBとCとDを通る3次曲線でBとCをつなぎ、BとCとDとEを通る3次曲線でCとDをつなぎ、といった作業を繰り返すと、計算量を抑えつつわりとなめらかなグラフを描ける。しかし、この方法で得られるグラフには（各サンプルを境に）まだ角張りがある。
そこで、さらになめらかな（連続した）グラフができる方法が考えられた。先ほどは連続する4点の座標から3次方程式を得たが、代わりに、連続する2点の座標とその両端のグラフの傾き（1次導関数の値）と曲率（2次導関数の値）から3次方程式を得るという方法である（他にも方法があるかもしれないが筆者は知らない）。筆者はあまりよく理解していないのだが、上記は簡単な行列演算で求まるらしい。
この方法をスプライン補間（今挙げたものは、3次式を使うので3次スプライン補間）といい、やはり両端の点が（代入すべき隣の点の傾きや曲率が存在しないため）計算上問題になるのだが、これは計算者が任意に決めてしまうらしい（曲率＝0と仮定するのを自然スプラインといって、普通これが利用される）。
ここまで見てきた補間法を、まとめて多項式補間という。
ここまででかなりなめらかな曲線を得る方法が得られたが、別の切り口として、フーリエ変換を利用する方法もある。
グラフィック処理ではフーリエ変換の特殊形である離散コサイン変換が多く用いられるが、音声データの場合、もともとアナログ関数とШ関数（くし型関数：パルス波のグラフになる関数で、周期的デルタ関数とも）を乗算してPCMデータを得ていることから、元のアナログ波形にШ関数をかけてさらにある関数をかけると元の波形に戻る、という関数を探すことになる。
で、元のアナログ関数f(t)と、f(t)にШ関数をかけたものをそれぞれフーリエ変換して見比べると、矩形関数を掛け算してやればよいことがわかるらしい（理論的な理由はさておき、Ш関数と矩形関数（矩形波をグラフにしたもの）は見た目に「形が逆」っぽいので、なんとなくわかならいでもない）。
ということで矩形関数をかけてフーリエ逆変換で元に戻してやると、矩形関数だった部分はy = sin(πx)/πxという形になっており、これをsinc関数（sine cardinalの略）という（形としては、インパルスに帯域制限をかけたような格好：sinc(0)は定義できないので1で代用することが多い）。sinc関数を使った補間法はsinc補間と呼ばれる。
ちなみに、関数の考え方で補間するやり方を「カーネル法」といい、そのとき用いる関数を「補間カーネル」と呼ぶことがある。また、sinc関数をフーリエ変換すると矩形関数に、矩形関数をフーリエ変換するとsinc関数になるが、このような関係をフーリエ変換対という。
sinc補間は理論上元のアナログデータを完全に復元するはずなのだが、1つ困ったことがある。
というのは、sinc関数はゼロでない値が無限に続く（コンパクトサポートでない、と表現する）関数なので、本当にsinc関数を使って計算すると演算量が無限大になっていつまでも終わらない。
そのため、sinc関数に類似したコンパクトサポートな関数（sinc関数に窓関数をかけたものが多く、windowed sinc関数などと呼ぶ）で代用することになる。代用する関数によって、cubic補間だとかLanczos補間などといったものがある。フーリエ変換を有限の計算量で打ち切った場合に誤差が出る（とくに、波形が角張って倍音が豊富な部分に出やすい）ことをギブズの現象というが、sinc補間でも同様の現象が見られる（ギブズの現象については情報通信のメモというサイトの解説が詳しい：暗に矩形関数をフーリエ展開したとき誤差を念頭に言うこともあるし、数学では不連続点の値が左右極限の相加平均になる現象を指す）。
ちなみに、サンプリングにより時間軸方向に輪切りにしたデータから元の波形を復元する意味で、sinc補間を行うことを「ローパスフィルタをかける」と表現することがある。実際、デジタルデータに理想的なsinc補間を施した場合と、補間なしのデータに理想的な（周波数特性が矩形の）ローパスフィルタをかけた場合で、最終的に得られる出力は同じ（元の波形と一致する）である。
なお実装を考えると、コンパクトサポートでないこと自体はあまり問題でなく、時間領域での収束が遅いことが問題になる。どういうことかというと、デジタルで処理する限り、正負の無限大への極限が0であれば＝±∞で収束すれば（という表現で問題がないのかどうか自信がないが）有限時間で量子化ノイズに埋もれるからである。実際、sin(πx)は-1から1までの値しか取らないので、1/πxが最下位ビットの半分より小さくなれば、sin(πx)/πxをデジタルデータに変換しても0以外の値を取らなくなるはずである。
Audacityでは、サンプルレート変換にsinc補間（に近似したもの）を利用している。設定の項目で「高品位」とあるのは、多分計算量を増やして精度を上げたものだと思う。波形は1次補間で表示されているが、実際にはローパスがかかってから再生されるので、リサンプリングしても音が大きく変わることはない（「表示」と「発音」で違う処理をしていることに注意）。
efuさんのWaveGeneで作成した250Hz@8KHzサンプリングの正弦波と、それをAudacity（高品位設定）で48KHzにリサンプリングしたものをスペアナにかけてみた
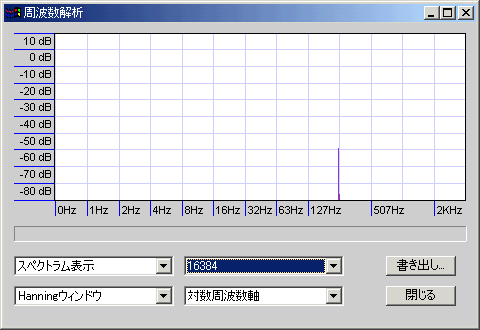
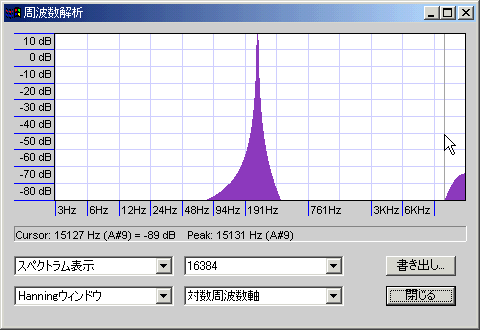
音程がややぼけて高域にノイズが乗っているが、まずまずキレイな特性。高音ノイズは-80db@17.6KHzだったので、可逆圧縮してしまえば落ちる程度である。もう少しキリの悪い周波数で、6300Hz@8KHzサンプリングの正弦波と、それをAudacity（高品位設定）で48KHzにリサンプリングしたものも試してみた。波形はかなりキレイになり、
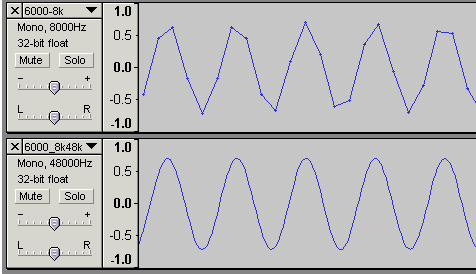
100Hz辺りに-80db程度のノイズが入っているが、あとは250Hzのときと似たようなもの
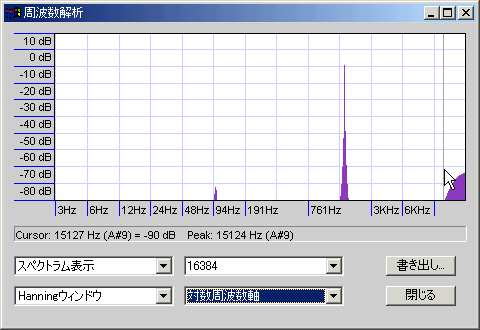
サンプルファイルも用意した（後ろに妙な無音が入っているのがリサンプリング済みファイル：Audacityで処理するとなぜか無音が入る）が、ブラインドで聴き分けられる人はいるだろうか。
もし十分に時間をかけてリサンプリングすることが可能であれば（当然ノンリニア編集に限られるが）、PCMのサンプルレートは記録可能周波数の上限を定めるのみで、それ以外の音質にはほとんど影響しないはずである（詳しくは一足飛びの妙な誤解を解消したいのページを参照）。
ただし、パルス波、鋸波、矩形波など、有限計算量でフーリエ変換を打ち切ると波形が乱れるものについては、それなりの誤差が出る。デジタルシンセから折り返し雑音をタレ流したままの波形を出力した場合は、波形の暴れ方が大きくなる（波形変化自体はあまり問題でないが、ピーク音圧が暴れると不便）。以下は6300Hz@44.1KHzサンプリングの鋸波（折り返しノイズに相当する成分もタレ流し）を48KHzにリサンプリングした波形。
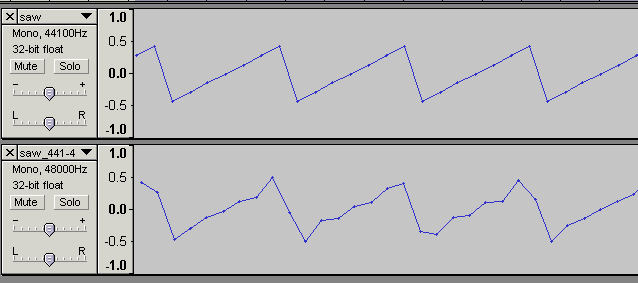
波形自体はかなり乱れており、スペアナを見ると-70dbのホワイトノイズ＋音程のぼやけといったところか。
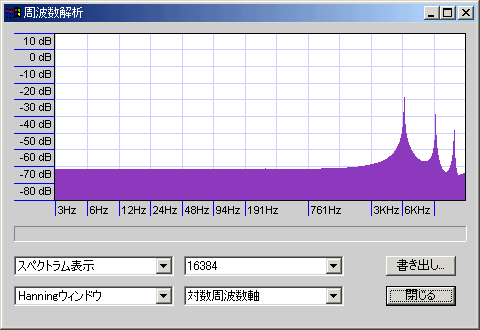
音声的になにか問題があるような変化ではないはずだが、サンプルファイルに音声データを同封してあるので、心配性な人は各自確認して欲しい。
また、周波数が高く一定でかつ単純な波形をデジタルシンセから出力して記録する場合にも注意が必要である。たとえば、3600Hzの純粋な正弦波を8000Hzサンプリングで録音すると、サウンドカードの仕様によってトレモロがかかったような妙な音が再生されることがある。これは記録の問題ではなく再生の問題で、スプライン補間など多項式系の補間方法だと避けようがない。ただし、デジタルシンセの出力を単品で再生する場合くらいしか問題にならない（いわゆるキラーソース）ので、実用上は気にしなくても大丈夫。
余談になるが、上記を「アップコンバートで音質が上がる」などといった話と混同しないで欲しい。適切な補間をしないと音質が下がるだけであって、何倍にアップコンバートしたから音質が上がるとかいうことではない（現実的な計算量で理想的な補間に少しでも近い実装として、アップコンバートしてからローパスをかけるのが有効でない、と言いたいわけではないので誤解なきよう）。
ぶっちゃけていうと、デジタル変換すると目立つノイズが入る（解像度の項を参照）ので、あらかじめ目立たないノイズを乗せておいてやる（すると目立つノイズは入らなくなる）という機能のこと。詳しくはAnonymousRiver Siteというサイトのディザを聴いてみようというページが非常に詳しいので、まともな知識を得たい人はそちらを参照。Audacityではビット深度（サンプルフォーマット）変換時にディザをかけている。
以下は、Aucacity1.2.6で無音トラックにディザをかけ、60db増幅したもののスペアナ表示である。同じスペアナ結果を数値化したものも一応用意した。一応、読み込みと増幅加工時にはディザを「なし」に設定している。
矩形ディザ
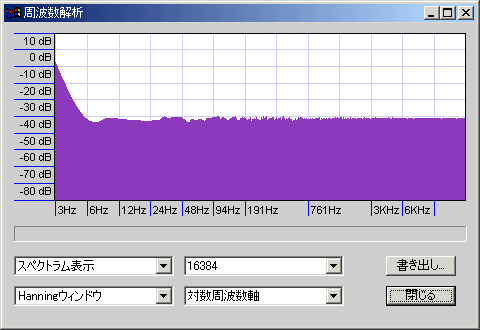
三角ディザ
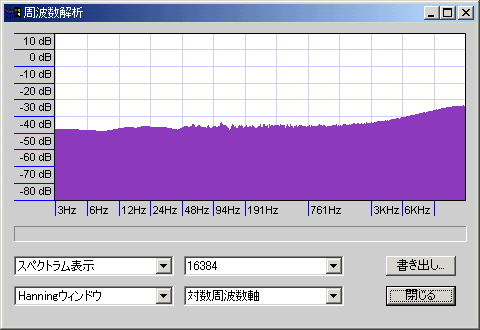
成形ディザ
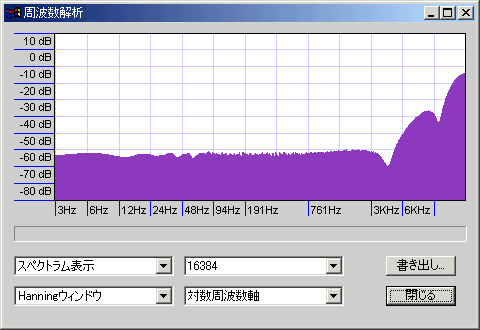
だいたい、矩形は-100db程度のホワイトノイズ＋極低域に山（音圧のピークレベル-90db：矩形窓だと低域のノイズは見えない）、三角は-105db程度のホワイトノイズ＋高域になだらかな山（ピークレベル-84db）、成形は-120db程度のホワイトノイズ＋高域に大きな山（ピークレベル-65db）になっている。関数窓によるノイズもあるため、実際のノイズレベルは多少異なることに注意。
Audacityバージョン1.26の場合、矩形ディザは2値（-1と0が同じ頻度で出現する＝確率分布が矩形になる）、三角ディザは5値（-2と-1と0と+1と+2が1：2：3：2：1の頻度で出現する＝確率分布が三角形になる）だが、これ以外の実装ももちろんありえる（確率分布としては矩形と三角形のほかにガウス分布などが使えるし、場合によっては3値の矩形ディザが有効な場面もあるだろう）。
成形は高域の山が2段になっているが、1段目のピークは-95db@9.5KHz程度、2段目は-99db@14KHz・-93db@15KHz・-87db@16KHz・-83db@17KHz・-79db@18KHz・-77db@19KHz・-78db@20KHzくらい（20KHzを超えるまで-75db以上の値はほとんど出現せず、24KHz近くでも-72db程度）。三角の山は3KHzくらいから始まり、6KHzくらいで-100dbを超え、最大で-92dbくらいである。
14KHzくらいまでの性能（ノイズの少なさ）は成形が圧勝で、それより上は多少ノイジーでも影響が少ない（ラウドネス曲線の影響で微小音は聴こえない）。可逆圧縮する場合は17～19KHzあたりでバッサリと高域がカットされるのでなおさらである。ただし、ディザが「重ねがけ」されると性能を発揮できなくなる（そもそも「16bitのディザが重ねがけされない」ように編集すべき）。いづれにせよ最終段（Audacityで32bit編集していたものを16bitに書き出すとき）の出力には成形が向くといえる。矩形ディザは高域ノイズが何か問題を引き起こすときや処理の軽さが求められるとき、三角ディザは（何か特殊な都合で）重ねがけ回数が非常に多くなるときに使えるが、最終段の出力には使わなくてよさそうに思える。
なお、サンプルレートを96KHzにすると成形ディザの高域の山がそれだけ高域に移動するが、
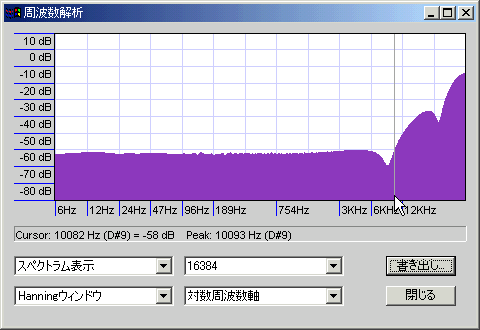
サンプルレート192KHz（バージョン1.2.6現在、Audacityでは対応していない）で編集できれば、高域の山（20KHz以上）を丸ごとローパスフィルタで削ることが可能だと思われる（ただし、そんなところで頑張ってもビット深度の影響の方が圧倒的に大きいので、実用上のメリットはないはず）。何度も繰り返しているが、32bitのディザならどんな種類のものを何回かけようと、通常ありえる範囲での問題は起きようがないし、そもそも24bitくらいよりも深いビット深度ではディザの必要性がない（最下位ビットで構成されるノイズがどんな分布をしていても問題にならないから）。
周波数によって指向性が変わるが、カタログに載っているのは、たいてい1KHzのサイン波に対する値である。
無指向性マイクは、空気の圧力（の変化）を読み取ればよい。音をさえぎる要素がなく、ダイヤフラムが十分小さければ、前後左右どこから来た音波でも同様に読み取れるはずである（少なくとも理論上は）。
マイクの正面（軸）と音源からマイクまでを結んだ直線のなす角をθとして感度をrで表すと、どの方向にも一定の感度なのだから、r=sとなる（sは定数）。つまり、音源の方向は感度に関係ない。
双指向性マイクは、ある面における空気の（前後の）移動速度を読み取ればよい。真横からの音波は空気を前後に揺らさないため感度ゼロになる。斜めからの音波は三角比で前後方向の速度を取り出したものが読み取り音圧になる。
音源までの距離が十分遠くかつ周波数が十分低いと、正面からでも感度がゼロになる。このことからわかるように、指向性マイクの近接効果というのは、本来的には「近距離で低音の感度が上がる」現象ではなく「遠距離で低音の感度が下がる」現象である（詳しくは用語のページを参照）。
無指向性マイクのときと同様に式にすると、r=s*cosθとなる。マイクの正面を上にすると、8の字のような指向になる。このとき、8の字の下半分は位相が逆になっていることに注意が必要。
無指向性マイクと双指向性マイクの両方を用意してそれぞれ読み取った音を加算してやると、双指向性マイクが拾った音のうち8の字の下半分（マイクの正面の反対側）は位相が逆なので無指向性マイクが拾った音と打ち消しあい、上半分（マイクの正面側）は位相が同じなので単純に加算される。
結果的に、指向性がマイクの正面側に偏った形になる。無指向性マイクのときと同様に式にすると、r=s(1+cosθ)となる。
このとき、双指向性マイクが拾った音を増幅してから加算してやると、つまりr=s(1+q*cosθ)（ただしqは1以上の定数）としてやると、さらに指向性が増す。ただし、マイクの正面と反対方向に逆位相の感度を持つことになる。
ちょうど耳に手をかざして特定方向からの音だけを聴くときのように、集音用の筒を取り付けて指向性を持たせたマイク。狙った方向の音だけをスポット的に拾えるが、使いこなすのは難しい（らしい）。
音楽用では、ドラムスの中から特定の音を拾い上げる（ライドシンバルだけとか）場合に使うことが多い。