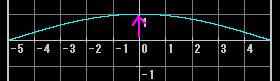
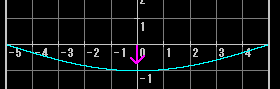
2倍音の振動は以下のようになっている
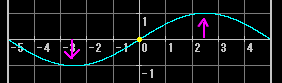
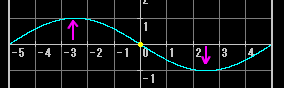
ちょうど真ん中に「動きのない点」(=図中黄色の点で「振動の節」という:これに対して動きが最大になる点=図中の紫の矢印を「振動の腹」という)があって、弦の両端と同じ働きをしていることがわかる。3倍音の振動も一応掲載
倍音振動に不動点があるというのはマグネティックピックアップで弦の振動を拾うときに重要で、ピックアップの位置によって特定の周波数に対するゲインが上下する。
筆者はド文系で、高校程度の数学も怪しいところがたくさんあり、変なことを書いている可能性があるので注意。
このページにあるスクリーンショットの一部は、YKさんのBearGraphの画面を利用している。使いやすい関数のグラフ化ソフトを公開なさっている作者の方に、この場を借りて謝辞を申し上げる。
まずは、両端を固定した弦の中央部分を引っ張ってそれを放すという状況を考えてみる。ギターなどを想像するとわかりやすいだろう。弦を放すと、引っ張られていた弦は元に戻ろうとするが、勢い余って反対側へ行き過ぎてまた戻ってくる。そしてまた戻り過ぎては行き過ぎてを繰り返し、結局振動を続けることになる。
このとき、過渡的な振る舞いを記述するには微分方程式を解く必要があるが、振動が落ち着いた状態だけ考えるなら、かなり簡単な式で済む。結論からいえば、振動の周期(固有周波数f)が、f={1/(2*l)}*{(T/σ)^(1/2)}で与えられる(fは周波数、lは長さ、Tは張力、σは線密度(単位長さあたりの質量)で、単位はそれぞれHz、m、N、kg/m)。つまり、軽いand/or張力が強い弦ほど、高い周波数で振動する。
実は、最初に弦を放した瞬間は、かなり無秩序にいろいろな周波数の音が混じりあっている。というか、インパルスと呼ばれる「すべての周波数において同じパワー」の波形に、いくらか似た感じになる(弦の形自体は、三角形から台形を経由して反対側に行くような運動になる)。アナログ出力がインパルスであることは「0時間で全エネルギーが放出される」(振幅は無限大)のと同義で、完全なインパルスを発生させる物質はもちろん存在しないが、なにかを叩いたり弾いたりしてすぐに制動すると似たような出力になる。
弦楽器の弦をミュートせずに弾くと、まずインパルスにローパスをかけたような振る舞いを示し、固有周波数fの整数倍でない成分が素早く減衰して、弦の固有周波数fとその整数倍の周波数を持った(つまり整数倍音の)振動だけが持続する。素早く減衰する成分があるのは、たとえば、弦がまだ右に動こうとしているのに左方向へ力が加わっても、全体として弦の動きが遅くなるだけで、戻ってきてまた行くという連鎖に発展しないからである。
弦の運動エネルギーは音響エネルギーに変換されて放出されるだけでなく、一部は熱になって逃げる。このとき、弦が硬い(変形に対する抵抗が大きい)と、高次倍音など振動長が短い成分は比較的早く減衰する。図については次の項に譲るが、一般に、振幅が同じなら高次倍音ほど大きな変形を要する。
弦の固有周波数fと同じ振幅の振動(弦の動き)が以下のようになっているとすると、


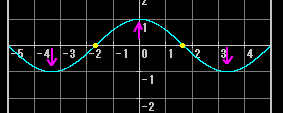
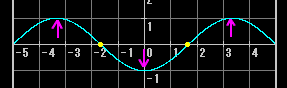
2倍音の振動は以下のようになっている


ちょうど真ん中に「動きのない点」(=図中黄色の点で「振動の節」という:これに対して動きが最大になる点=図中の紫の矢印を「振動の腹」という)があって、弦の両端と同じ働きをしていることがわかる。3倍音の振動も一応掲載


倍音振動に不動点があるというのはマグネティックピックアップで弦の振動を拾うときに重要で、ピックアップの位置によって特定の周波数に対するゲインが上下する。
1倍音と2倍音では振動の腹が違うため、弦の中央を引っ張って放すと2倍音が少ない音色、やや端寄りを引っ張って放すと2倍音が多い音色になる。また、弦の中央を指などで押さえたうえで弦の端から1/4または3/4の場所を引っ張って放すと、1倍が出ずにと2倍音(とその倍音)だけが出る(すぐに指を放さないと2倍音も消える:ギター族でいうハーモニクス、バイオリン族ではフラジオレットと呼ばれる)。これも不動点が影響しており、弦の中央に触れると1倍音には制動がかかるが、2倍音には(理想的には)影響がないことを利用したもの。
1倍音と、その半分の強さの2倍音が出ているときの弦の動きは次のようになるが、
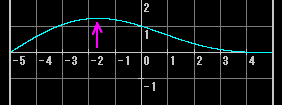
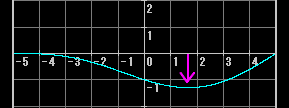
2倍音が1倍音の1/4の強さに減衰すると次のようになる(運動の中心が弦の中央に寄ったのがわかる)。
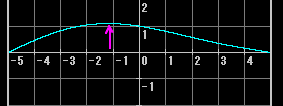
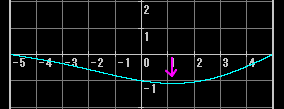
ただし前の項でも触れたように、上の図は弦の振動をイメージとして示したもので、振動している弦の形がこのようになっているわけではないことに注意して欲しい。
上記では両端が固定端(文字通り、固定されている)となっている場合を想定したが、片方が自由端(文字通り、自由に動ける)となっている場合はどうか(定規の片端を持ってもう片方の端を弾いてやる様子を想像するとよい)。これは、同じ長さで両端が固定端である振動体と比べて固有周波数fが半分になる(下の図は本来の振動と少し違うのだが、面倒なことになるのでこれで勘弁していただきたい)
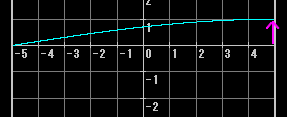
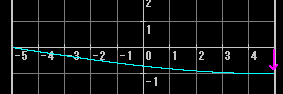
この場合、偶数倍音は発生しない(というか持続しない)
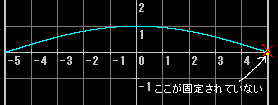
奇数倍音は発生(持続)する。たとえば3倍音なら以下のようになる
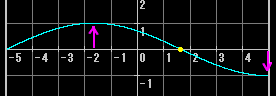
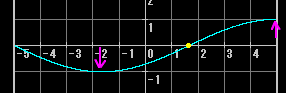
ひも状の物質に張力をかけて振動させた場合、完全な倍音は出ない(音程がズレて高くなる)。これをインハーモニシティという。弦の「硬さによって自由に振動できない部分」の長さが周波数(というか分割振動の細かさ)によって変わることが影響しているようだ(硬い弦を弱く振動させるほど強く影響し、柔らかい弦を強く振動させると影響が弱まる)。
ピアノ概論というサイトの解説によると、K = 3.3 * 10^15, d = 弦の直径(mm), l = 弦長(mm), f = 振動周波数(Hz)とした場合、インハーモニシティの比率δ = (K * (d^2)) / ((l^4) * (f^2))となり、実際の音程のズレT(cent)は、n倍音に対してT = n^2 * δになるらしい(アルアンダーソン博士という人の公式だそうな)。google電卓を使うなら「((3.3 * (10^15)) * (d^2)) / ((l^4) * (f^2)) =」に代入するとδを計算できる。fを固定して考える(=同じ音程の音で比較する)と、弦の直径が太く弦長が短いほどインハーモニシティが大きく、弦の直径が細く弦長が長いほどインハーモニシティが小さいことになる。
この公式はピアノ用のものらしいが、ギターのような小型の楽器の場合なかなかすごい数値になる。たとえば650mmスケールのギターにライトゲージの6弦(直径1.37mmのスチール弦:レギュラーチューニングだとE2=82.4Hz)を張った場合δ=5.11となり、2倍音で20セントも差が出ることになる(4倍音のE4に至っては80セントも高くなる:そういえば、ギターをレギュラーチューニングにすると1弦開放には6弦開放がよく共振するが、6弦開放に対して1弦開放はあまり共振しないような気がする)。
ためしに手元のサイレントギターをスペアナに通してみたところ、エクストラライトゲージ6弦開放(かなり使い古した弦、ライン録音)の基音が82Hzで4倍音が333Hzだった(3回測って3回とも同じ数字)。本来の4倍音は328Hzのはずだから、音程にすると26セントの違いで、計算ほど大げさな差ではなかった。また11倍音も922Hzで38セントのズレと、やはりピアノの公式ほど大きな差にならなかった。ピアノ線が張ってあることには変わりなくても、楽器によって事情がかなり違うようだ(弦の柔軟性が影響しているのだろう)。いづれにせよ、出音をセント単位で分析すると、ピアノよりはギターの方がズレやすいらしい(ギターのコードフォームがルートを極力重ねるようになっているのはこのせいなのかもしれない)。
上記の理屈でレギュラーチューニングに限定して考えると、コントロールできるパラメータは弦の太さだけなので、大きいゲージの弦を高いテンションで張るとインハーモニシティ大、小さいゲージの弦を低いテンションで張るとインハーモニシティ小ということになる(ただし、あまりダルダルのテンションにしても音が狂うし、バキバキのハイテンションにしすぎると楽器が壊れるので、限度はある)。またハイフレットほど「実質的な弦長」が短くなるので、インハーモニシティも相応に大きくなるのだろう。面白そうなのでそのうち実験してみたい。
ギターにしろピアノにしろ、上記の倍音のズレはその楽器の音として普通に認識されているもので、音が狂っているのとは少し事情が違う。インハーモニシティが小さいと柔らかめの、大きいと緊張感のある音色になるとよく言われる。また使い古した弦は倍音が非常に小さくなる(東京スタジオというスタジオのサイトで公開されている実験結果がわかりやすい)。また、ピアノをはじめとする鍵盤楽器の調律カーブを検討する際にも、インハーモニシティが考慮される。
音波を円筒に通してやると面白いことが起こる。空気(に限らず流体)中における音波というのは疎密波(縦波)で、空気の密度が変わることによって伝わるのだが、ここで、疎密波は「伝わるだけ」なら「仕事」をしない(ただし空気の抵抗で熱に変わる分を無視できる距離において)ということに注目する。
まずは、十分に細く音を外部に漏らさない円筒の一端にスピーカ(音源)を取り付けて、もう一端にマイク(人間の耳でもよい)を置く場合を考える。スピーカからはホワイトノイズが出ているとしよう。

実質的には、スピーカが(空気を介して)マイクを押し引きする形になっているのだが、マイクが動かされる(空気が仕事をする)際には当然抗力が発生する。つまり、空気がマイクを押せばマイクは空気を押し返すし、空気がマイクを引っ張ればマイクは空気を引っ張り返す。そしてこの抗力は、最終的にスピーカのところまで伝わる。
ここで、管の長さをl(m)、音速を340(m/s)とすると、スピーカからマイクに力が伝わるまでの時間はl/340(s)、仕事を受けたマイクからスピーカに抗力が伝わるまでの時間もl/340(s)となる。結局、スピーカが(空気に対して)仕事をしてからマイクからの抗力を受け取るまで2l/340(s)の時間がかかることになるが、ここではこの時間をT(s)としよう。
スピーカが空気を押したT秒後に、スピーカが再び空気を押していた場合、スピーカの力と抗力が互いに打ち消しあうことになる。反対に、スピーカが空気を押したT秒後に、スピーカが空気を引っ張っていた場合、スピーカの力と抗力は同じ向きになる(ので、結果的にスピーカの動きが増幅される)。
ということは、時間Tの間にスピーカの振動が0.5・1.5・2.5・3.5...周期進めば、スピーカは効率よく仕事をし、そうでなければ音波が減衰するということになる。つまり、340/4lを固有周波数として、その奇数倍の倍音が出てくることになる。ちょうど自由端がある場合で取り上げた例とほぼ同じ結果になる(ただし、伝達ロスの分とマイク内部で電気や熱に変わる分、スピーカの力よりも抗力の方が弱いので、偶数倍音も少しは残る)。
では、マイクが管の端から離れていた場合はどうだろうか。

この場合も、仕事をする相手がマイクから筒の外の空気に変わっただけで大きな変化はない(本当はインピーダンスなどを考慮しなければならないようだが、この際無視)。
スピーカと管の間にわずかな隙間を作ると、ちょっと変化が出る

この場合、時間Tの間にスピーカの振動が1・2・3・4...周期進むと、E1ではスピーカからの力とE2からの抗力が逆向きに鉢合わせることになるが、これは合算されてE1から外部へ向けた力として作用する(結局増幅される)。いっぽう、時間Tの間にスピーカの振動が0.5・1.5・2.5・3.5...周期進む場合、E1では仕事がなされない。つまり、E1からは340/2lHzの音とその倍音が強く出て、E2からはあまり音が出ない(音量が小さいだけで、出ないことはない)。よって340/2lHzを固有周波数として、その整数倍の倍音が出てくることになる。図のE1~E2の区間にある空気は結局「ばね」として機能している。ちなみに、リコーダーの指穴を全部塞いで音を出すと下の穴から低音が聞こえるのは、上記でいうE2からの音。
さらに、筒の途中に穴をあけて、そこを塞いだり塞がなかったりすると、筒の長さを変えたのと同じ効果になる

上の図はリコーダーの構造とほぼ同じで、疎密波の圧力はE3から逃げるため、それより先の筒にはあまり伝わらない(空気の抵抗があるため、やはり、まったく伝わらないわけではない)。E1から直接漏れる音や、E2から出る音があるため、比較的複雑な(ノイズが多い、と言ってもよい)波形になる。
上記において、スピーカ(発音体)と筒の間に隙間がない場合を閉管、隙間がある場合を開管といって、前者の例としてクラリネット、後者の例としてリコーダーやフルートがある。円筒を通して音を伝えるとは言いつつも、円筒の中の空気の振動が音色に深く関わっている(コムフィルタに近い役割を果たしている)。
ちなみに、音速は温度と気圧によって変わる(1気圧では摂氏温度をtとして331.5+0.61t、正確には、比熱比をk、気体定数をR、絶対温度をTとして√kRTで表す)ので温度が変わると筒(の中の空気)の固有周波数も変わる。たとえば摂氏30度で固有周波数が100Hzの閉管(長さ0.8745m≒87.5cm)があったとして、温度が摂氏0度に下がると固有周波数は約94.77Hzになる。
ここまでは弦や笛の類ばかり扱ってきたが、楽器の発音体には膜状のものもよくある。振動モードとモード周波数という考え方で扱うのが普通で、深大寺しんぷるてくのろじ~研究所というサイトの解説が詳しい。
これもよくわからないのだが、紐や膜と決定的に異なるのは1点で支持できることだろう(板を薄くすれば膜になるし、膜を細くすれば弦になるため、連続的ではある:たとえばカホンの打面にごく薄い板を使ったら普通の太鼓に近い構造になる)。鉄琴や木琴は一般に2点支持だが、管楽器用のリードやオルゴールの櫛歯は1点支持する。
叩いて音程のある音を出す場合端から22.4%の点を振動の節にすることが多いようで、鳴るほど!楽器解体全書(ヤマハ)のチェレスタの紹介にもそのような記述がある。上記リンク先の説明は興味深く、板が厚いと音が高くなるとか、両端に錘をつけて長さを節約する場合があることなども紹介されている(錘の利用は、木琴の音板の裏を削るのと似たような発想なのだろう)。
開管/閉管の決定的な違いは、発音体の直近に空気の逃げ場があるか否かであったが、円錐(メガホン状の筒)の場合はどうなるのか。詳しい事情はよくわからないのだが、低い周波数の音に対してのみ閉管に近い振る舞いをするらしい(面音源として振舞う距離でのみ影響があるということなのかな?)。
さらに、筒が外側にめくれながら広がるホーン形状の場合、広がり係数と呼ばれる値を用いるようで、狭い方の口の断面積をS0(cm^2)として、口からの距離d(m)における断面積S=S0 * e^(d * m)とするそうな(eは自然対数の底、mが広がり係数)。無限長ホーンではカットオフ周波数fc=m * c / 4π(Hz)を境に低域が落ちる、ということのようだ。
今度は、片方が閉じた筒もしくは壷状の入れ物に音をぶつけてみる(スピーカと入れ物の距離は十分近いものとする)。
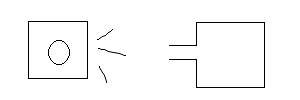
すると今度は、空気の逃げ場がないために、入れ物の中の空気は単純にバネとして作用する(容積が小さければ高音と、大きければ低音と共鳴する)。ギターのサウンドホールやバスレフ方式のスピーカなどに応用される技術で、ヘルムホルツ共鳴器という(筆者は詳しいことを知らないのでリンク先のページを参照)。
またこのとき、空気ばねとしての作用だけでなく普通の「筒」としての作用も(小さいながら)同時に生じており、その影響はポートの長さに支配される(閉管として振る舞う)。
このような「開口部のある箱」は共鳴箱(弦楽器の胴やチェレスタの共鳴箱など)として使うこともできるし、直接叩いて音を出す(ウッドブロックやカホンなど)こともできる。開口部のない箱も共鳴箱として利用でき、スピーカ用の密閉エンクロージャが端を固定したばね、バスレフエンクロージャが端におもりをつけたばね(もう一端はスピーカユニットに接続され、これも一端が固定されたバネとして扱う)として機能することが、上記リンク先で紹介されている。
音を出す本体(発音体)には、空気の通過によるもの(リード:気鳴楽器)、紐状のもの(ストリングス:弦鳴楽器)、膜状のもの(太鼓:膜鳴楽器)、固体(太鼓以外のパーカッションのほとんど:体鳴楽器)などがある。
リードには、エアリード(口笛の原理)、ダブルリード(草笛の原理)、リップリード(リード板の代わりに唇を使う)、シングルリード(ダブルリードの片方を固定したもの)、フリーリード(リードをぶつけずにそのまま振動させる)などがある。弦楽器には、弦を撥じくもの、弓などでこするもの、ハンマーでたたくものなどがある。
共鳴装置は、発音体が出した音を成形するとともに音響インピーダンス(後述)の変換を行う。チェレスタのように発音体の音響インピーダンスがある程度高いものは独立した共鳴箱を持っていることもあるが、弦楽器の多くは音響インピーダンスを変換する表板や響板と共鳴箱が一体化した構造のものが多い。すでに紹介したようにコムフィルタのような効果を持つものが多く、フィードバックのような効果で発音体の動き自体もある程度変わる。
筒状もしくは箱状のものがほとんどで、長さを変えたり(金管とか:発音体が出す音の周波数が安定しないため、共鳴装置の方で周波数を決め打ちしている)3次元構造を利用したり(ピアノとかギター族とかヴァイオリン族とか:発音体が出す音の周波数が安定しているため、共鳴装置の特性が比較的曖昧)して広い音域に対応しているものもあれば、音階ごとに別の共鳴装置をもつもの(マリンバとかビブラフォンとか)もある。竪琴の一部(ごく原始的なもの)やトライアングルやクラベスなど共鳴装置がない楽器もなくはない。リュラー(同じ名称の楽器が複数あるが、ここではギリシアのリュラーを指し、馬蹄型の箱(板に見えるが中空らしい)の開口部に棒を渡したような形状の竪琴で、ブリッジを介して箱に弦を固定するところがハープ類と異なる:神話上はヘルメースの発明でアポローンの持物とされ、デュオニッソスの笛と対比される)、キタラー(リュラーの一種(発展形)で、リュラーの共鳴板に枡を被せて共鳴箱にしたような形:ギターやチターの語源と言われる)など、弦の振動を箱に伝えて共鳴させる方法はかなり早くから利用されていたようだ。
箱と筒の違いを構造で考えると、開口部がないものが密閉箱、1つのものが開口箱、2つのものが筒、箱と筒をくっつけて都合開口部が1つになったものor密閉箱に小さい開口部を設けたものがバスレフ箱、ということになる。さらに、開口部に膜を張るとダブルヘッドの太鼓のようになる(三味線の胴はこのような構造が多く、すでに紹介したように膜と板との違いは連続的なので、ギターの胴(裏板が膜と板の中間のような特性になる)なども似たような振る舞いをすると思われる:ブレージングと呼ばれる補強で板としての性質を強めているのが普通)。すでに紹介したように、筒(の中の気柱)は錘付きばね、箱(の中の空気)は一端を固定したばねとして振る舞う。
音響インピーダンスは音圧を体積速度で除したもの(オームの法則で、電圧を電流(時間あたりに移動する電子の数)で割ると抵抗がわかるのと同じ)で、物理単位として考えると(Pa)÷(m^3/s)だからPa・s/m^3になる。体積速度というのは面積と粒子速度の積で、単位はm^2×m/sでm^3/s、ぶっちゃけた理解としては「時間当たりに移動する流体の体積」を示す。PaはN/m^2と同義なのでPa・s/m^3=N/m^2・s/m^3=N・s/mであり、対象が流体でない場合はN・s/mで扱うことが多い(機械インピーダンスと呼ばれる)。また、平面進行波の音圧を粒子速度で除したものは特性インピーダンスと呼ばれ、単位はPa・s/mになる(面積を考慮しなくてよい=線速度で考えられるため、分母の次数が減る)。
これらは(電気のインピーダンスと同様に)波動の伝わり方を示しており、音響インピーダンスが低い=小さな音圧でも大量の空気が動く、音響インピーダンスが高い=大きな音圧でも少量の空気しか動かない、ということだと考えて(とりあえず)問題ない。楽器の発音体と共鳴装置の関係を考えるなら、運動する部分の面積が小さいとハイインピーダンスで、大きいとローインピーダンスになると解釈してよいだろう(空気に対してどれだけ効率よく仕事をする/されるかという問題なわけで、団扇を前後に動かす場合と左右に動かす場合/団扇の広い面に風を吹きつける場合と側面に風を吹きつける場合を想像してみるとよい)。
たとえばアコギの場合、弦自体の投影面積はかなり小さい。つまり、大きな振幅で運動しても、たいした量の空気は動かせない。そこで駒(ブリッジ)を介して振動を胴に伝えてやると、表板は弦に比べてはるかに面積が広いので、効率よく空気を動かせるようになる(と同時に、弦の運動エネルギーがどんどん音波に変わるので、サステインは短くなる:さらに、外部からの音波が弦に直接する仕事はたいしたものでないが、表板に対しては効率よく仕事をするため、結局は駒を介して弦を動かすことになる)。なお、駒から表板に音が伝わる際の機械インピーダンスは弦の振動方向で変わり、表板と垂直な弦の振動はより伝わりやすく、表板と水平な弦の振動はより伝わりにくい(クラシックギターなどでは基本技術とされる)。
表板や響板が極端に硬く重い(たとえば大きなコンクリートの塊に硬い駒を打ち込んで弦を張るとか)と、板はほとんど振動しない(弦を振動させてピックアップで拾う電気楽器ならあり得る方法だが、表板を振動させて音を伝えるアコースティック楽器には不向き)。板が極端に薄い(たとえばギターの表板の代わりにドラムヘッドのようなものを高い張力で張るとか)と、膜としての振る舞いが強まり上下振動よりも変形振動の方が強くなる(側板や裏板の重さにもよる)。板が極端に軽く硬い(たとえば硬いプラ板に駒を打ち込んで弦を張るとか)と板の上下振動が大きめになり、もし質量を無視できるくらい軽く剛体とみなせるくらい硬ければ、板から弦への抗力は空気抵抗だけになる(実際には支持方法で振る舞いが変わる)。板が極端に柔軟(たとえば丈夫な合成ゴムの板に駒を打ち込んで弦を張るとか)だと周波数の高い成分が板の内部で熱に変わる(駒の位置が一定しないので音程も曖昧になる)。実際の楽器では、変形振動とハイ落ちのバランスや面積と重さの兼ね合いなどを考慮して板の形状や材質が決められている。
ここで注意が必要なのは、板が重く硬いときに振動の減衰が最小で、柔らかいと微分値が大きいほど(=周波数が高いほど)振動が熱に変換され、軽いと微分値が小さいほど(=周波数が低いほど)エネルギーが板の上下振動になって逃げ、変形が大きいと板が変形振動するということだろう。ギター族やヴァイオリン族のようにネックのある弦楽器の場合、板の変形振動とともにネックの振れも生じるため、扱いが複雑になる。とくにソリッドギターではボディよりもネックの方が薄く長いため影響が顕著で、弦をミュートしたままボディを叩くより、ヘッドを叩いた方がピックアップに大きな音が入力されることもある。
余談だが、ギター(エレキでも可)の裏板やネック裏などに耳をくっつけて音を出すと、胴やネックが震えているのがよくわかる(インドのヴィーナ(リュートやギターに似た楽器だが、もともとは「弦楽器」一般を指したらしい)など、ヘッドやネックにも共鳴装置を取り付けた楽器もある:同じくインドの楽器でシタールにも、共鳴装置を取り付けることがある)。
金属の振動を電磁誘導で電気信号に変えるマグネティックピックアップ(エレキギターはたいていこれ:電磁誘導が起こらないガットやナイロンには使えず、アコギ弦として一般的なブロンズもあまり適さないため、ニッケルなどを主体とした専用弦を使う)、(ブリッジや共鳴装置などに取り付けて)振動による圧力の変化を拾う圧電ピックアップ(圧電気を英語でpiezoelectricityということからピエゾピックアップとも:マグネティックピックアップよりも出力が弱くまた低音が弱くなりがちなため、たいていプリアンプがついている)、空気の振動を拾うエアマイク(名前の通り、本来はピックアップでなくマイクロフォン(コンタクトマイク)に分類すべきだが、慣例的にピックアップとして扱われることが多い)などがある。共鳴装置の表面に取り付けるタイプの圧電ピックアップはコンタクトピックアップと呼ばれることが多い。最近はレーザーで弦や音板の振動を読み取る光学ピックアップの話も聞くが、2010年現在、市販の楽器に採用された話は聞いたことがない。ちなみに、水晶振動子(クオーツ)も圧電効果を持つ(圧電気を生じる)素子なのだが、ピエゾ素子には入れないことが多い。
アクティブ回路(能動素子を使った回路のことで、能動回路とも:能動素子の定義は明確でないが、成型タイプの(単純な分割でない)エネルギー変換を行う素子のことで、真空管やトランジスタがこれに当たる)を備えたものと、パッシブ回路(受動素子のみを使い能動素子を使っていない回路で、受動回路とも:受動素子の代表例は、コイル・コンデンサ・トランス・レジスタなど)を備えたものに分類されることがあるが、理論だけ考えると、これはプリアンプ(とプリアンプの電源)が本体についているか外部機器のプリアンプを使うかという差でしかない(ノイズ対策を考えるなら前者が優れている)。ただし、ピックアップの質自体が違う(具体的には、高音が減衰しにくいピックアップを採用して効率の低さをアンプで補うなど:コイルの巻数=インダクタンス=効率(感度)=高い周波数に対するインピーダンス=高音の減衰度だと考えてよい)こともある。
マグネティックピックアップでは共鳴装置をもっぱら弦の振動を変化させる目的(実際的にはピップアップ自体が共鳴装置にマウントされることが多いので、その影響も考慮しなければならない)で使用し、それ以外の音作りはイフェクタやアンプを使って行う。光学ピックアップならば、発音体の運動がほぼ完全に自由になる(マグネティックピックアップでは運動エネルギーを電気的エネルギーに変換しているため、感度を上げるほどサステインが弱くなる:ピックアップの感度を下げられるアクティブ回路はこの点でも有利である)。またマグネティックピックアップ特有の事情として、ポールピースの真上に弦があり水平に振動しているとき基音が拾いにくいという特徴がある。これは弦が右へ行ったのと左へ行ったのを区別できないことによるもので、ポールピースの位置をずらすか弦の振動を垂直に近づけることで効果が小さくなる。またダブルポールピースにするとさらにクセが強まる(左右の振幅がポールピース幅を超えるか否かによって挙動が変わる)。
まったく倍音を含まない純粋な音はサイン波の形になる(聴覚検査で使う音や音叉の音が代表例)。あるサイン波に、2分の1の強さの2倍音、3分の1の強さの3倍音、4分の1の強さの4倍音・・・と整数倍音を(無限に)重ねていくと、のこぎりの歯のような波形になり、これをのこぎり波(鋸波)という。また、奇数倍音だけを選んで足し合わせていくと矩形波(長方形の波という意味)になる。実際の波形などについては詳しい解説を載せているサイトがあるのでそちらを参照。
本来は、のこぎり波や矩形波にフーリエ展開(フーリエ変換を有限区間で行うもので、任意の波を複数のサイン波の重ね合わせとして把握する:詳しい解説を載せているサイトがあるので知りたい人はそちらを参照)という作業を施すことで結果的に上記の重ね合わせが得られる(矩形波の場合15倍音くらいまでは重ねないとそれっぽい形にならない)という理論がまず先にある(はず)。とりあえず、倍音の少ない音色は丸みのある、奇数倍音の多い音色は四角っぽい、整数倍音成分が多い音色はのこぎり状の波形になりやすいということは覚えておいて損はない。直感的な理解には、Pixelさんのピストンコラージュというソフトに付属しているピストンボイスという波形エディタが大いに役立つだろう。
ともかく、のこぎり波や矩形波は整数/奇数倍音を豊富に(というか無限に)含んでいるため、これにハイパスフィルターやローパスフィルターをかけてやることで任意の整数/奇数倍音成分を取り出すことができる(減算方式のアナログシンセがこれを実際にやっている:この方式だと整数/奇数倍音でない成分は表現できない)。
上記以外でよく用いられる波形としては、三角波(サイン波を尖らせたような波形)、パルス波(完全なパルス波だと、音圧が00001000010000100001のような値になる)、非対称矩形波(パルス波と矩形波の中間:矩形波の「山」を細くしたような波形)などがある。パルスはかなり曖昧な語で「極端なデューティー比を持つ非対称矩形波」「短時間の急峻な変化を規則的に繰り返す波形」「補間しないPCMのようなブロック状の波形」など、広義な捉えられ方をすることがある。
参考までに、efuさんのWaveGeneというオシレータソフトで発生させた各波形(すべて250Hzで-3dbピーク)をAudacityで拡大表示したものを掲載しておく。
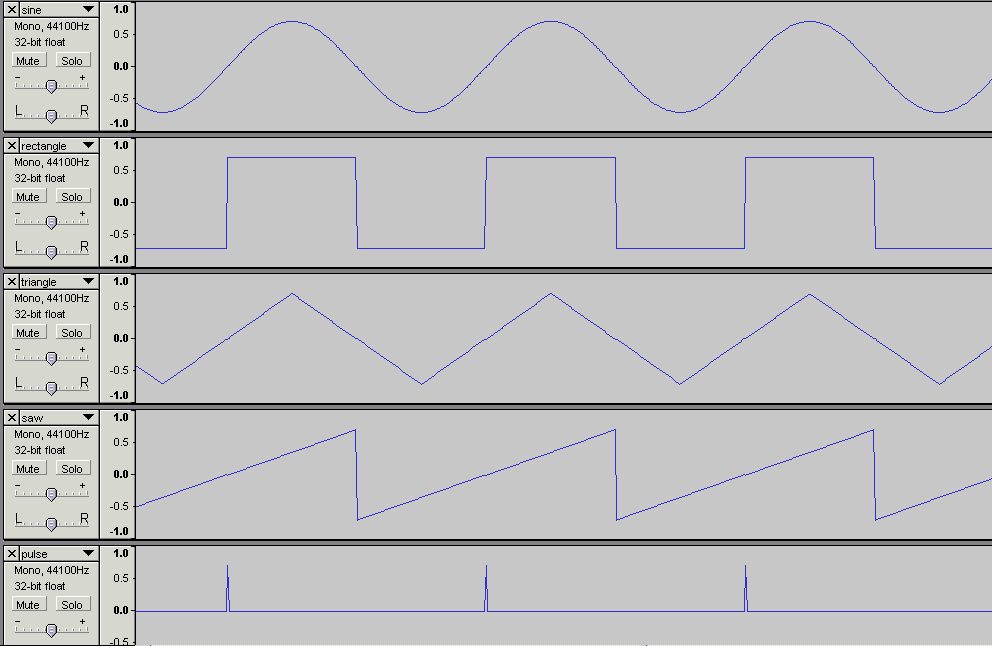
上から順に、サイン波・矩形波・三角波・鋸波・パルス波。音声のサンプルファイルも一応用意した(再生できない場合はNorthern Verse さんのSoundPlayer Lilith などを使うとよい)。
なお、音波を時間tに従って音圧が変化する関数f(t)に見立てると、微積分などで処理が可能になる(いづれの場合もDCオフセットは無視して考えるのが普通)。矩形波を微分すると両側パルス波(ただし音圧無限大で面積1)、矩形波を積分すると三角波、三角波を積分すると三角に近いクネっとした波形になる。周波数で考えると、波形を時間で積分することはローパスフィルタをかける(=高音を弱める)のと同じなので、両側パルス波の周波数を上に行くほど弱くすると矩形波、さらに弱くすると三角波ができることになる(cos(x)を積分してもsin(x)のままだが、cos(2x)を積分すると1/2*sin(2x)になる:置換積分が必要なので詳しくは数学の教科書を参照、元がコサイン波であってもサイン波であっても周波数n倍で積分後の振幅が1/n倍になる=約6db/octのローパスになるのは変わらない)。鋸波はちょっと性質が異なり、微分すると片側パルス波、積分すると放物線をツギハギした波形になる。
波動関数の微積分は結局、周波数に応じてパワーを削る操作であって、元の波形にない周波数成分(「歪み」と呼ばれる)が生成されることは(演算が正確であれば)ない。歪みを意図的に作り出す操作もいろいろとあり、たとえば正弦波を半波整流すると、2・4・6・8・10倍音と、弱い12・14倍音が現れる。全波整流すると基音のスペクトルがゼロになり、結果的に周波数2倍の鋸波に近い形になる。全波整流した波形からDCオフセットを取り除かずにファズをかける(クリップさせる)と非対称矩形波と鋸波の中間のような形になる。変調をかけることで複雑な周波数成分をもった波形を生成する手法もある。
一般に扱われる音声信号について真面目に考えると、自分が何階にいるのかわからなくなってくる。
たとえばエアマイクでは、圧力勾配型のムービングコイルマイクも速度型のベロシティマイクも検出しているのは圧力や位置ではなく変化の割合で、マグネティックピックアップも磁界の変化を検出する。つまり空気粒子や弦の位置が微分される。これをスピーカやヘッドフォンで再生すると、また積分されて元に戻る。
たとえば「ちょうど三角波と同じ動き」で振動している鉄弦が(実際にはあり得ないが)あったとする。これをマグネティックピックアップで拾うと磁界の変化は矩形波様になるはずで、ピックアップの出力もそれを反映することになる。同じ信号をスピーカに入れると、電圧がプラスのところではコーンが前に、マイナスのところではコーンが後ろに動いて、元の三角波に(それぞれのセクションで誤差はあるものの)戻る。
これが圧力や位置を直接検出する方法、たとえばコンデンサマイク(静電容量は位置で決まる)や圧電ピックアップの場合、そのままだと微分されない(ハイパス/ローカットフィルタを通らない)信号が出てくるはずである(多分)。またスピーカでは、電圧が電流になって力になって加速度になって速度になって変位になって空気が押し引きされているはずである(きっと)。
まあいづれにせよ、一般に扱う音声信号は電圧または電圧を符号化したものに違いなく、微分器や積分器が必要な装置にはあらかじめそれらが実装されているだろうから、深くは気にしないでよさそうにも思える。
周波数が近い音を重ね合わせると、位相が揃って増幅される時間と位相が揃わず打ち消しあう時間が周期的に現れ、トレモロイフェクトやAM変調などをかけたような波形になる。
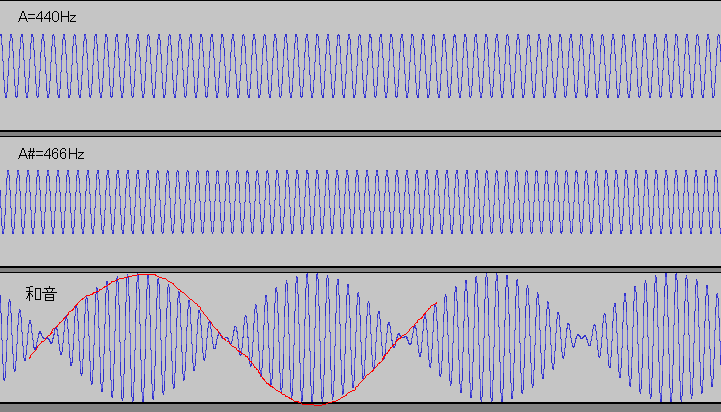
図は上から順に、A=440Hzのトーン、A#=466Hzのトーン、それら2つを重ね合わせたもの。再生すると下の図の赤線が示す低音が出ているように聴こえ、うなりとかbeatなどと呼ばれる。赤線は青線の山1つ1つに接する曲線で、このような関係を「赤線の曲線は青線の曲線群の包絡線である」という(詳しくはその他のページを参照)。
周波数が簡単な整数比になる音同士でも、メカニズム的にどこまで同一視できるのかよくわからないが、重ね合わせると見かけ上低音が発生することに変わりはない。
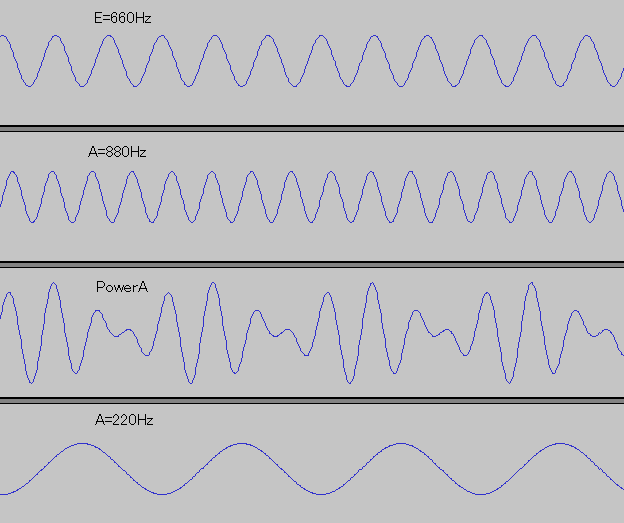
図は上から順に、E=660Hzのトーン、A=880Hzのトーン、2つを重ね合わせた和音(PowerA)、A=220Hzのトーン。Aから見るとEは完全5度、Eから見るとAは完全4度なのだが、2つを重ね合わせた和音は(周波数が低い)Eではなく(周波数が高い)Aがルート音扱いになると、和音のページで述べた。
その理由は下2つの波形に注目するとわかる。
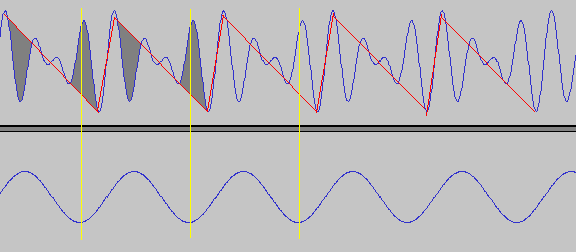
和音の波形は、ちょうどAのトーンと同じ周波数の鋸波と三角波の中間くらいの波(図の赤線)に、やはりAのトーンと同じ周波数のパルス波に近い波(赤線と青線の差分:図の濃いグレー部分)を足したような波形になっている。つまり、660HzのEと880HzのAを重ね合わせると、見かけ上220HzのA(に倍音を乗せた音)が発生することになる。
これらの低音を音程根音(Interval Tonic)といい、ヘルムホルツという人の結合音の研究をヒンデミットという人が応用してまとめた理論(の一部)で説明されるらしい。式で書くと、faとfb(fa<fb)の2音を重ね合わせた場合fc=fb-faとなる「うなり(beat)」(これ以外にもいろいろとあるらしく、この式で表される音は第一次差音というらしい)が発生する、ということになる(音波には下方倍音が存在する、という主張はこれを錯覚したもののようだ)。音程根音が可聴周波数域を下回っている場合、音程としてではなく音量のうねり(トレモロのような効果)として知覚される。
これとは別に歪成分耳音響放射という現象があって、耳の中で能動的にこの低音を増幅する効果もあるのだが、それについてはオーディオの重箱の隅のページで触れる。
以下に、1000Hzと1414.21Hzの和音(上:典型的な不協和音であるトライトーン)と1000Hzと2000Hzの和音(下:典型的な協和音であるオクターブユニゾン)の波形を示した。
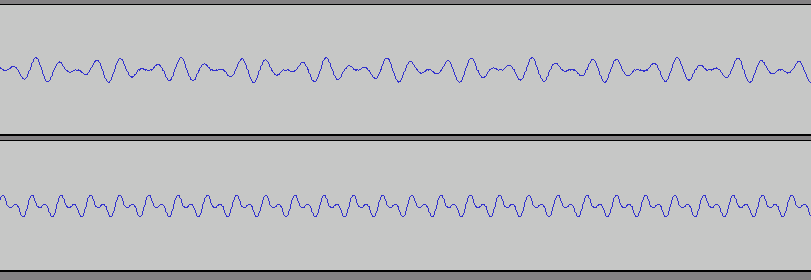
協和音では規則正しい波形が続いており、不協和音では波形が一定せず常に形が変わっているのがわかると思う。
この波形の不安定さが、トライトーンが不協和音になる正体だと思われる。音の特徴が不定形で、何が倍音で何が基底音なのか把握できないことが不安感に繋がるのだろう。
十分に長い時間観察すると、周波数の比が有理数になる純音同士の波形はどこかでループするはずであるが、このループ1周期にかかる時間がある程度より長いと、やはり似たような不安感がある(周波数の比が無理数である場合、理論的には、ループなしで常に異なる波形が続く)。このことは、周波数の比が同じでも音程が低いほど濁った和音に聞こえるという現象に関与しているのではないかと思う(確証は何もないが)。